题目内容
11. 如图,在平行四边形ADBO中,圆O经过点A、D、B,如果圆O的半径OA=4,那么弦AB=4$\sqrt{3}$.
如图,在平行四边形ADBO中,圆O经过点A、D、B,如果圆O的半径OA=4,那么弦AB=4$\sqrt{3}$.
分析 由四边形ADBO是平行四边形,OA=OB,有一组邻边相等的平行四边形是菱形,得到?ADBO是菱形,证得AB,OD互相垂直平分,再由勾股定理求得结果.
解答  解:∵四边形ADBO是平行四边形,
解:∵四边形ADBO是平行四边形,
∵OA=OB,
∴?ADBO是菱形,
∴AB,OD互相垂直平分,
∴OC=$\frac{1}{2}$OD=$\frac{1}{2}$OA=2,
∴AC=$\sqrt{{OA}^{2}{-OC}^{2}}$=2$\sqrt{3}$,
∴AB=2AC=4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 本题考查了菱形的判定和性质,勾股定理的应用,圆的性质,熟记同圆的半径相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.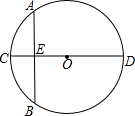 在⊙O上作一条弦AB,再作一条与弦AB垂直的直径CD,CD与AB交于点E,则下列结论中不一定正确是( )
在⊙O上作一条弦AB,再作一条与弦AB垂直的直径CD,CD与AB交于点E,则下列结论中不一定正确是( )
 在⊙O上作一条弦AB,再作一条与弦AB垂直的直径CD,CD与AB交于点E,则下列结论中不一定正确是( )
在⊙O上作一条弦AB,再作一条与弦AB垂直的直径CD,CD与AB交于点E,则下列结论中不一定正确是( )| A. | AE=BE | B. | $\widehat{AC}$=$\widehat{BC}$ | C. | CE=EO | D. | $\widehat{AD}$=$\widehat{BD}$ |
19.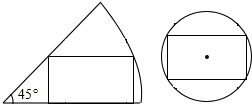 一张圆心角为45°的扇形纸板和一张圆形纸板分别剪成两个大小相同的长方形,若长方形长和宽的比值为2:1,则扇形纸板和圆形纸板的半径之比为( )
一张圆心角为45°的扇形纸板和一张圆形纸板分别剪成两个大小相同的长方形,若长方形长和宽的比值为2:1,则扇形纸板和圆形纸板的半径之比为( )
 一张圆心角为45°的扇形纸板和一张圆形纸板分别剪成两个大小相同的长方形,若长方形长和宽的比值为2:1,则扇形纸板和圆形纸板的半径之比为( )
一张圆心角为45°的扇形纸板和一张圆形纸板分别剪成两个大小相同的长方形,若长方形长和宽的比值为2:1,则扇形纸板和圆形纸板的半径之比为( )| A. | 2$\sqrt{2}$:1 | B. | $\sqrt{5}$:1 | C. | 2:1 | D. | $\sqrt{2}$:1 |
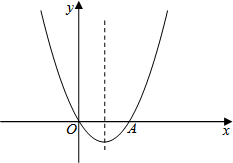 如图,已知关于x的二次函数y=x2+mx的图象经过原点O,并且与x轴交于点A,对称轴为直线x=1.
如图,已知关于x的二次函数y=x2+mx的图象经过原点O,并且与x轴交于点A,对称轴为直线x=1.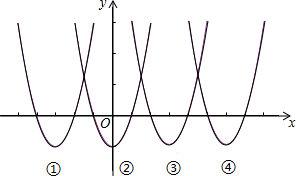 如图为函数:y=x2-1,y=x2+6x+8,y=x2-6x+8,y=x2-12x+35在同一平面直角坐标系中的图象,其中最有可能是y=x2-6x+8的图象的序号是第三个.
如图为函数:y=x2-1,y=x2+6x+8,y=x2-6x+8,y=x2-12x+35在同一平面直角坐标系中的图象,其中最有可能是y=x2-6x+8的图象的序号是第三个.