题目内容
16.解方程组:(1)$\left\{\begin{array}{l}{4x-3z=17}\\{3x+y+5z=18}\\{x+2y+z=2}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x-2y=-9}\\{y-z=2}\\{3z+x=5}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{4x-3z=17①}\\{3x+y+5z=18②}\\{x+2y+z=2③}\end{array}\right.$,
②×2-③得:5x+9z=34④,
①×3+④得:17x=85,即x=5,
把x=5代入①得:z=1,
把x=5,z=1代入③得:y=-2,
则方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=-2}\\{z=1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x-2y=-9①}\\{y-z=2②}\\{3z+x=5③}\end{array}\right.$,
①+②×2得:x-2z=-5④,
③-④得:5z=10,即z=2,
把z=2代入②得:y=4,
把z=2代入③得:x=-1,
则方程组的解为$\left\{\begin{array}{l}{x=-1}\\{y=4}\\{z=2}\end{array}\right.$.
点评 此题考查了解三元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
7.2015年1月1日起,杭州市城区实行全新的阶梯水价,之前为了解某社区居民的用水情况,随机对该社区20户居民进行了调查,下表是这20户居民2014年8月份用水量的调查结果:那么关于这次用水量的调查和数据分析,下列说法错误的是( )
| 居民(户) | 1 | 2 | 8 | 6 | 2 | 1 |
| 月用水量(吨) | 4 | 5 | 8 | 12 | 15 | 20 |
| A. | 平均数是10(吨) | B. | 众数是8(吨) | C. | 中位数是10(吨) | D. | 样本容量是20 |
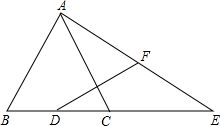 如图,已知在△ABC中,AB=AC=2$\sqrt{5}$,sin∠B=$\frac{2\sqrt{5}}{5}$,D为边BC的中点,E为边BC的延长线上一点,且CE=BC.联结AE,F为线段AE的中点.
如图,已知在△ABC中,AB=AC=2$\sqrt{5}$,sin∠B=$\frac{2\sqrt{5}}{5}$,D为边BC的中点,E为边BC的延长线上一点,且CE=BC.联结AE,F为线段AE的中点.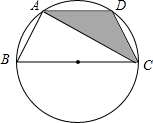 如图,已知点A、B、C、D均在以BC为直径的圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10,则图中阴影部分的面积为$\sqrt{3}$.
如图,已知点A、B、C、D均在以BC为直径的圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10,则图中阴影部分的面积为$\sqrt{3}$. 如图,在平行四边形ADBO中,圆O经过点A、D、B,如果圆O的半径OA=4,那么弦AB=4$\sqrt{3}$.
如图,在平行四边形ADBO中,圆O经过点A、D、B,如果圆O的半径OA=4,那么弦AB=4$\sqrt{3}$.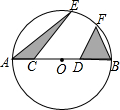 如图,⊙O的半径为6,AB是⊙O的直径,C、D是AB的三等分点,∠ECB=∠FDB=60°,则图中阴影部分的面积是6$\sqrt{11}$.
如图,⊙O的半径为6,AB是⊙O的直径,C、D是AB的三等分点,∠ECB=∠FDB=60°,则图中阴影部分的面积是6$\sqrt{11}$.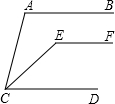 已知:如图AB∥CD,EF∥CD,CE平分∠ACD,∠A=110°,则∠CEF=145°.
已知:如图AB∥CD,EF∥CD,CE平分∠ACD,∠A=110°,则∠CEF=145°.