题目内容
6. 如图,⊙O的半径为1cm,弦CD的长度1cm,弦AC、BD所夹的锐角α为75°,则弦AB的长为$\sqrt{2}$.
如图,⊙O的半径为1cm,弦CD的长度1cm,弦AC、BD所夹的锐角α为75°,则弦AB的长为$\sqrt{2}$.
分析 首先证明△ODC是等边三角形,得到∠DBC=$\frac{1}{2}$∠DOC=30°,根据α=∠DBC+∠ACB,得到∠ACB=75°-30°=45°,所以∠AOB=2∠ACB=90°,在RT△AOB中利用勾股定理即可求出AB.
解答 解:如图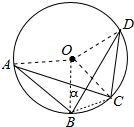 ,连接OA、OB、OC、OD、BC.
,连接OA、OB、OC、OD、BC.
∵OD=OC=CD=1,
∴∠DOC=60°,
∴∠DBC=$\frac{1}{2}$∠DOC=30°,
∵α=∠DBC+∠ACB,
∴∠ACB=75°-30°=45°,
∴∠AOB=2∠ACB=90°,
在RT△AOB中,∵OA=OB=1,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{2}$,
故答案为$\sqrt{2}$.
点评 本题考查圆周角定理、等边三角形的判定和性质、等腰直角三角形的判定和性质、勾股定理等知识,解题的关键是发现等边三角形这个突破口,充分利用特殊三角形解决问题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
15.一个正多边形的内角和与其外角和之和是1440°,则这个正多边形的一个外角的度数为( )
| A. | 36° | B. | 45° | C. | 55° | D. | 60° |
16.“嫦娥三号”探测器于2013年12月2日1时30分发射,“嫦娥三号”携“玉兔号”月球车首次实现月球软着落和月面巡视勘察,“嫦娥三号”进入远地点高度约38万公里的地月转移轨道.380000公里用科学记数法表示为( )
| A. | 38×104 | B. | 3.8×105 | C. | 3.8×104 | D. | 38×105 |
 阿春准备在如图所示的边长为1的正方形网格中,作一个三边长分别为4,5,$\sqrt{17}$的△ABC,他已经作出了其中的一条边,请你帮他把这个三角形补充完整.
阿春准备在如图所示的边长为1的正方形网格中,作一个三边长分别为4,5,$\sqrt{17}$的△ABC,他已经作出了其中的一条边,请你帮他把这个三角形补充完整.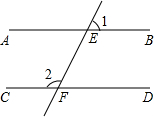 如图,已知AB∥CD,EF分别交AB、CD于点E、F,∠1=70°,则∠2的度数是110°.
如图,已知AB∥CD,EF分别交AB、CD于点E、F,∠1=70°,则∠2的度数是110°.