题目内容
4.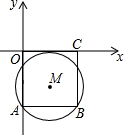 如图,在平面直角坐标系中,正方形ABCO的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切,若点A的坐标为(0,-4),则圆心M的坐标为( )
如图,在平面直角坐标系中,正方形ABCO的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切,若点A的坐标为(0,-4),则圆心M的坐标为( )| A. | (-2,2.5) | B. | (2,-1.5) | C. | (2.5,-2) | D. | (2,-2.5) |
分析 过M作MN⊥AB于N,连接MA,设⊙M的半径是R,根据正方形性质求出OA=AB=BC=CO=8,根据垂径定理求出AN,得出M的横坐标,在△AMN中,由勾股定理得出关于R的方程,求出R,即可得出M的纵坐标.
解答 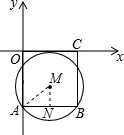 解:∵四边形ABCO是正方形,A(0,-4),
解:∵四边形ABCO是正方形,A(0,-4),
∴AB=OA=CO=BC=4,
过M作MN⊥AB于N,连接MA,
由垂径定理得:AN=$\frac{1}{2}$AB=2,
设⊙M的半径是R,则MN=8-R,AM=R,由勾股定理得:AM2=MN2+AN2,
R2=(4-R)2+22,
解得:R=$\frac{5}{2}$,
∵AN=2,四边形ABCO是正方形,⊙M于x轴相切,
∴M的横坐标是2,
即M(2,-$\frac{5}{2}$).
故选D.
点评 本题考查了勾股定理、切线的性质、正方形性质,垂径定理等知识点,本题综合性比较强,是一道比较好的题目.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
15.一个正多边形的内角和与其外角和之和是1440°,则这个正多边形的一个外角的度数为( )
| A. | 36° | B. | 45° | C. | 55° | D. | 60° |
16.“嫦娥三号”探测器于2013年12月2日1时30分发射,“嫦娥三号”携“玉兔号”月球车首次实现月球软着落和月面巡视勘察,“嫦娥三号”进入远地点高度约38万公里的地月转移轨道.380000公里用科学记数法表示为( )
| A. | 38×104 | B. | 3.8×105 | C. | 3.8×104 | D. | 38×105 |
13.2013年10月6日开幕的第六届东亚运动会共招募了6800名志愿者,某服装加工厂为这些志愿者赶制服装,若每天按原计划制作服装,则要比规定的时间晚6天完成;若每天比原计划多制作34件,则比规定的时间早4天完成,求原计划每天制作服装的件数.若设原计划每天制作x件服装,依题意,下面所列方程正确的是( )
| A. | $\frac{6800}{x}$-6=$\frac{6800}{x+34}$+4 | B. | $\frac{6800}{x}$+6=$\frac{6800}{x+34}$-4 | ||
| C. | $\frac{6800}{x+34}$-6=$\frac{6800}{x}$+4 | D. | $\frac{6800}{x+34}$+6=$\frac{6800}{x}$-4 |
14.有两根7cm、10cm的木棒,要想以这两根木棒做一个三角形,可以选用第三根木棒的长为( )
| A. | 3cm | B. | 11cm | C. | 20cm | D. | 24cm |
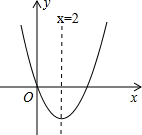 二次函数y=x2+bx的图象如图所示,对称轴为x=2,若关于x的一元二次方程x2+bx-t=0(t为实数)在-1<x<6的范围内无解,则t的取值范围是t<-4或t≥12.
二次函数y=x2+bx的图象如图所示,对称轴为x=2,若关于x的一元二次方程x2+bx-t=0(t为实数)在-1<x<6的范围内无解,则t的取值范围是t<-4或t≥12. 如图,△ABC中,AB=8,AC=10,BC=12,D、E分别是AB、AC的中点,则△ADE的周长是15.
如图,△ABC中,AB=8,AC=10,BC=12,D、E分别是AB、AC的中点,则△ADE的周长是15.