题目内容
2.某中学八(1)班体育老师对班上一个组学生进行跳绳测试并规定:每分钟跳100次以下的为D等;每分钟跳100~109次的为C等;每分钟跳110~119次的为B等;每分钟跳120次及以上的为A等.测试结果整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:
(1)参加这次跳绳测试的共有20人;在扇形统计图中,D类所对应的圆心角的度数是54°;
(2)补全条形统计图;
(3)该组达到A等级的同学中只有1位男同学,老师打算从该组达到A等级的同学中随机选出2位同学在全班介绍经验,请用列表法或画树状图的方法,求出所选两位同学恰好是1位男同学和1位女同学的概率.
分析 (1)利用C等级的人数除以它所占的百分比即可得到总人数,然后用D等级的百分比乘以360°得到D类所对应的圆心角的度数;
(2)先计算出A等级和B等级的人数,然后补全条形统计图;
(3)先画树状图展示所有12种等可能的结果数,再找出恰好是1位男同学和1位女同学的结果数,然后根据概率公式求解.
解答 解:(1)总人数=5÷25%=20(人),
D级学生的人数占全班总人数的百分数为:$\frac{3}{20}$×100%=15%,
扇形统计图中D级所在的扇形的圆心角为15%×360°=54°,
故答案为20,54°;
(2)B等级的人数=20×40%=8(人),A等级的人数=20×20%=4,
如图,
(2)画树状图如下:
共有12种等可能的结果数,其中恰好是1位男同学和1位女同学有6种情况:男女1,男女2,男女3,女1男,女2男,女3男,
所以恰好是1位男同学和1位女同学的概率=$\frac{6}{12}$=$\frac{1}{2}$.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了统计图.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
12.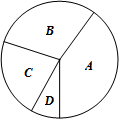 学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为A、B、C、D四类.A类表示非常了解;B类表示比较了解;C类表示基本了解;D类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为A、B、C、D四类.A类表示非常了解;B类表示比较了解;C类表示基本了解;D类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
(1)表中 m=,15; n=0.4.
(2)根据表中数据,求出B类同学数所对应的圆心角的度数.
(3)学校在开展了解校训意义活动中,需要将D类的甲、乙、丙、丁四名同学分成两组,每两人一组,求D类4个人中甲乙两人分成一组的概率是多少?(请用列表法或是树状图表示)
 学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为A、B、C、D四类.A类表示非常了解;B类表示比较了解;C类表示基本了解;D类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为A、B、C、D四类.A类表示非常了解;B类表示比较了解;C类表示基本了解;D类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:| 类别 | A | B | C | D |
| 频数 | 20 | m | 11 | 4 |
| 频率 | n | 0.3 | 0.22 | 0.08 |
(2)根据表中数据,求出B类同学数所对应的圆心角的度数.
(3)学校在开展了解校训意义活动中,需要将D类的甲、乙、丙、丁四名同学分成两组,每两人一组,求D类4个人中甲乙两人分成一组的概率是多少?(请用列表法或是树状图表示)
7.世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微笑的无花果,质量只有0.000000076克,将0.000000076用科学记数法表示为( )
| A. | 7.6×108 | B. | 0.76×10-9 | C. | 7.6×10-8 | D. | 0.76×109 |
 抛物线y1=mx2+(m-3)x-3(m>0)与x轴交于A、B两点,且点A在点B的左侧,与y轴交于点C,OB=OC.
抛物线y1=mx2+(m-3)x-3(m>0)与x轴交于A、B两点,且点A在点B的左侧,与y轴交于点C,OB=OC.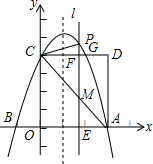 如图,二次函数y=ax2-2ax+4(a≠0)的图象交x轴于点A、B,点A坐标为(3,0),与y轴交于点C,以OC、OA为边作矩形OADC,点E位线段OA上的动点,过点E作x轴的垂线分别交CA、CD和二次函数的图象于点M、F、P,连接PC.
如图,二次函数y=ax2-2ax+4(a≠0)的图象交x轴于点A、B,点A坐标为(3,0),与y轴交于点C,以OC、OA为边作矩形OADC,点E位线段OA上的动点,过点E作x轴的垂线分别交CA、CD和二次函数的图象于点M、F、P,连接PC.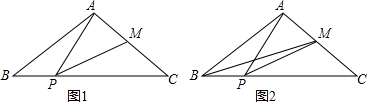 如图,在△ABC中,己知AB=AC=10,BC=16,点p在线段BC上运动(P不与B,C重合),连接AP,做∠APM=∠B,PM交AC于点M.
如图,在△ABC中,己知AB=AC=10,BC=16,点p在线段BC上运动(P不与B,C重合),连接AP,做∠APM=∠B,PM交AC于点M.