题目内容
在?ABCD中，E、F分别在DC、AB上，且DE=BF，四边形AFCE是平行四边形吗？说说你的理由．考点：平行四边形的判定与性质
专题：
分析：可由已知求证AF=CE，又有AF∥CE，根据一组对边平行且相等的四边形是平行四边形，可得四边形AFCE是平行四边形．
解答：答：四边形AFCE是平行四边形．
证明如下：∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD．
∵BF=DE，
∴AF=CE．
∵在四边形AFCE中，AF∥CE，
∴四边形AFCE是平行四边形．
证明如下：∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD．
∵BF=DE，
∴AF=CE．
∵在四边形AFCE中，AF∥CE，
∴四边形AFCE是平行四边形．
点评：本题考查了平行四边形的判定与性质．平行四边形的判定方法共有五种，应用时要认真领会它们之间的联系与区别，同时要根据条件合理、灵活地选择方法．
练习册系列答案
相关题目
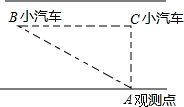“交通管理条例”规定：小汽车在城街路上行驶速度不得超过70千米/小时，如图，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路面车速检测仪A的正前方30米C处，过了2秒后，测得小汽车在B处与车速检测仪间距离为50米，这辆小汽车超速了吗？
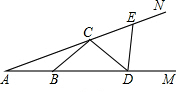如图，点B，D在射线AM上，点C，E在射线AN上，且AB=BC=CD=DE，已知∠EDM=84°，求∠A的度数．
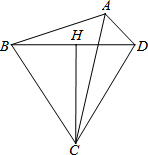已知：四边形ABCD中，∠ABC+∠ADC=180°，CH垂直平分BD