题目内容
8.如图,一次函数y=-2x的图象与二次函数y=-x2+3x图象的对称轴交于点B.(1)写出点B的坐标($\frac{3}{2}$,-3);
(2)将直线y=-2x沿y轴向上平移,分别交x轴于点C、交y轴于点D,点A是该抛物线与该动直线的一个公共点,试求当△AOB的面积取最大值时,点C的坐标;
(3)已知点P是二次函数y=-x2+3x图象在y轴右侧部分上的一个动点,若△PCD的外接圆直径为PC,试问:以P、C、D为顶点的三角形与△COD能否相似?若能,请求出点P的坐标;若不能,请说明理由.

分析 (1)只需先求出抛物线的对称轴方程,就可求出点B的坐标;
(2)如图1,由题意可设直线的解析式为y=-2x+b,要使△AOB的面积最大,只需直线DC与抛物线相切,由此可求出b的值,就可解决问题;
(3)过点P作PH⊥y轴,如图2.由题意可设直线的解析式为y=-2x+b,从而可得OC=$\frac{b}{2}$,OD=b,DC=$\frac{\sqrt{5}b}{2}$.由△PCD的外接圆直径为PC可得∠PDC=90°,易证△PHD∽△DOC,根据相似三角形的性质可得$\frac{PH}{DO}$=$\frac{DH}{CO}$=$\frac{PD}{DC}$.然后分两种情况讨论(①△PDC∽△DOC,②若△PDC∽△COD),用b的代数式表示出点P的坐标,然后代入抛物线的解析式,求出b,即可得到点P的坐标.
解答 解:(1)抛物线y=-x2+3x的对称轴为x=-$\frac{3}{2×(-1)}$=$\frac{3}{2}$,
当x=$\frac{3}{2}$时,y=-2x=-2×$\frac{3}{2}$=-3,
则点B的坐标为($\frac{3}{2}$,-3).
故答案为($\frac{3}{2}$,-3);
(2)如图1,
设直线DC的解析式为y=-2x+b,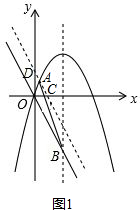
联立$\left\{\begin{array}{l}{y=-2x+b}\\{y=-{x}^{2}+3x}\end{array}\right.$,
消去y并整理得,
x2-5x+b=0,
当直线y=-2x+b与抛物线y=-x2+3x相切时,
△=(-5)2-4×1×b=25-4b=0,
解得b=$\frac{25}{4}$,
此时直线DC的解析式为y=-2x+$\frac{25}{4}$,
令y=0,可得x=$\frac{25}{8}$,
∴△AOB的面积最大时,点C的坐标为($\frac{25}{8}$,0);
(3)过点P作PH⊥y轴,如图2.
设直线的解析式为y=-2x+b,
则有C($\frac{b}{2}$,0),D(0,b),
从而可得OC=$\frac{b}{2}$,OD=b,DC=$\frac{\sqrt{5}b}{2}$.
∵△PCD的外接圆直径为PC,
∴∠PDC=90°,
∴∠PDH+∠ODC=90°.
∵∠DOC=90°,
∴∠OCD+∠ODC=90°,
∴∠PDH=∠OCD.
∵∠PHD=∠DOC=90°,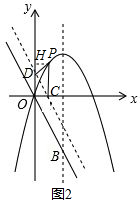
∴△PHD∽△DOC,
∴$\frac{PH}{DO}$=$\frac{DH}{CO}$=$\frac{PD}{DC}$.
①若△PDC∽△DOC,
则有$\frac{DP}{DC}$=$\frac{OD}{OC}$=2.
∴$\frac{PH}{DO}$=$\frac{DH}{CO}$=2,
∴PH=2DO=2b,DH=2CO=b,
∴OH=b+b=2b,
∴点P的坐标为(2b,2b).
∵点P在抛物线y=-x2+3x上,
∴2b=-(2b)2+3×(2b),
解得:b1=0(舍去),b2=1,
∴点P的坐标为(2,2);
②若△PDC∽△COD,
则有$\frac{DP}{DC}$=$\frac{OC}{OD}$=$\frac{1}{2}$.
∴$\frac{PH}{DO}$=$\frac{DH}{CO}$=$\frac{1}{2}$,
∴PH=$\frac{1}{2}$DO=$\frac{1}{2}$b,DH=$\frac{1}{2}$CO=$\frac{1}{4}$b,
∴OH=b+$\frac{1}{4}$b=$\frac{5}{4}$b,
∴点P的坐标为($\frac{1}{2}$b,$\frac{5}{4}$b).
∵点P在抛物线y=-x2+3x上,
∴$\frac{5}{4}$b=-($\frac{1}{2}$b)2+3×($\frac{1}{2}$b),
解得:b1=0(舍去),b2=1,
∴点P的坐标为($\frac{1}{2}$,$\frac{5}{4}$).
综上所述:点P的坐标为(2,2)或($\frac{1}{2}$,$\frac{5}{4}$).
点评 本题主要考查了抛物线的顶点、对称轴、抛物线上点的坐标特征、直线上点的坐标特征、相似三角形的判定与性质、圆周角定理、解一元二次方程、勾股定理等知识,运用分类讨论和构造K型相似是解决第(3)小题的关键.

| 用户序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 日用电量(度) | 4.4 | 4.0 | 5.0 | 5.6 | 3.4 | 4.8 | 3.4 | 5.2 | 4.0 | 4.2 |
(2)已知去年同一天这10户居民的平均日用电量为7.8度,请你估计,这天与去年同日相比,该小区200户居民这一天共节约了多少度电?
| A. | 调查某品牌电视机的市场占有率 | B. | 调查七年级一班的男女同学的比例 | ||
| C. | 调查某电视连续剧在全国的收视率 | D. | 调查某型号炮弹的射程 |
 如图,矩形OABC的边OA、OC在坐标轴上,反比例函数$y=\frac{k}{x}$(k为常数,且k>0)的图象在第一象限与BC、AB分别交于点M、N,直线MN与y轴交于点D,若$\frac{DM}{DN}=\frac{1}{4}$,记△BMN的面积为s1,△OMN的面积为s2,则$\frac{s_1}{s_2}$的值是$\frac{3}{5}$.
如图,矩形OABC的边OA、OC在坐标轴上,反比例函数$y=\frac{k}{x}$(k为常数,且k>0)的图象在第一象限与BC、AB分别交于点M、N,直线MN与y轴交于点D,若$\frac{DM}{DN}=\frac{1}{4}$,记△BMN的面积为s1,△OMN的面积为s2,则$\frac{s_1}{s_2}$的值是$\frac{3}{5}$.