题目内容
3. 如图,矩形OABC的边OA、OC在坐标轴上,反比例函数$y=\frac{k}{x}$(k为常数,且k>0)的图象在第一象限与BC、AB分别交于点M、N,直线MN与y轴交于点D,若$\frac{DM}{DN}=\frac{1}{4}$,记△BMN的面积为s1,△OMN的面积为s2,则$\frac{s_1}{s_2}$的值是$\frac{3}{5}$.
如图,矩形OABC的边OA、OC在坐标轴上,反比例函数$y=\frac{k}{x}$(k为常数,且k>0)的图象在第一象限与BC、AB分别交于点M、N,直线MN与y轴交于点D,若$\frac{DM}{DN}=\frac{1}{4}$,记△BMN的面积为s1,△OMN的面积为s2,则$\frac{s_1}{s_2}$的值是$\frac{3}{5}$.
分析 连接OB.首先根据反比例函数的比例系数k的几何意义,得出S△AON=S△COM=$\frac{1}{2}$k,然后根据平行线分线段成比例定理得出$\frac{CM}{BM}$=$\frac{DM}{MN}$=$\frac{1}{3}$,$\frac{BM}{BC}$=$\frac{3}{4}$,从而求得S△BOM=3S△COM=$\frac{3}{2}$k,S△BOC=S△AOB=$\frac{1}{2}$k+$\frac{3}{2}$k=2k,进一步求得S1=$\frac{9}{32}$×2S△BOC=$\frac{9}{32}$×4k=$\frac{9}{8}$k,最后由S△OMN=S矩形AOCB-S△AON-S△COM-S△BMN=4k-$\frac{1}{2}$k-$\frac{1}{2}$k-$\frac{9}{8}$k=$\frac{15}{8}$k得出结果.
解答 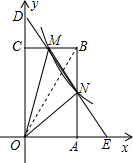 解:连接OB.
解:连接OB.
∵M、N是反比例函数$y=\frac{k}{x}$(k为常数,且k>0)的图象上的点,EA⊥x轴于A,FC⊥y轴于C,
∴S△AON=S△COM=$\frac{1}{2}$k.
∵$\frac{DM}{DN}=\frac{1}{4}$,
∴$\frac{DM}{MN}$=$\frac{1}{3}$,
∵AB∥OD,
∴$\frac{CM}{BM}$=$\frac{DM}{MN}$=$\frac{1}{3}$,
∴$\frac{BM}{BC}$=$\frac{3}{4}$,
∴S△BOM=3S△COM=$\frac{3}{2}$k,
∴S△BOC=S△AOB=$\frac{1}{2}$k+$\frac{3}{2}$k=2k,
∴S△BON=S△BOC-S△AON=2k-$\frac{1}{2}$k=$\frac{3}{2}$k,S矩形=4k,
∴$\frac{AN}{BN}$=$\frac{1}{3}$,
∴$\frac{BN}{AB}$=$\frac{3}{4}$,
∴$\frac{BM•BN}{BC•AB}$=$\frac{9}{16}$,
∴$\frac{\frac{1}{2}BM•BN}{BC•AB}$=$\frac{1}{2}$×$\frac{BM•BN}{BC•AB}$=$\frac{9}{32}$,
∴$\frac{{s}_{1}}{{s}_{矩形ABCD}}$=$\frac{9}{32}$,
∴S1=$\frac{9}{32}$×2S△BOC=$\frac{9}{32}$×4k=$\frac{9}{8}$k,
∵S△OMN=S矩形AOCB-S△AON-S△COM-S△BMN=4k-$\frac{1}{2}$k-$\frac{1}{2}$k-$\frac{9}{8}$k=$\frac{15}{8}$k.
∴$\frac{s_1}{s_2}$=$\frac{\frac{9k}{8}}{\frac{15k}{8}}$=$\frac{3}{5}$.
故答案是:$\frac{3}{5}$.
点评 本题是反比例函数的综合题,主要考查反比例函数的比例系数k与其图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系,即S=$\frac{1}{2}$|k|.得出$\frac{AN}{BN}$=$\frac{1}{3}$,$\frac{BN}{AB}$=$\frac{3}{4}$,是解决本题的关键.

 一次函数y=kx+b(k,b,k≠0)的图象如图所示,当y<0时,自变量x的取值范围是( )
一次函数y=kx+b(k,b,k≠0)的图象如图所示,当y<0时,自变量x的取值范围是( )| A. | x<-2 | B. | x>-2 | C. | x>2 | D. | x<2 |
| A. | 第一、三、四象限 | B. | 第一、二、三象限 | C. | 第二、三、四象限 | D. | 第一、二、四象限 |
| A. | 一组邻边相等的矩形是正方形 | |
| B. | 对角线互相垂直的平行四边形是菱形 | |
| C. | 等腰梯形的对角和相等 | |
| D. | 矩形的对角线互相垂直平分 |
| A. |  | B. |  | C. |  | D. |  |
