Question

18．有一块直角三角形绿地，量得两直角边长分别为3m，4m，现在要将绿地扩充成等腰三角形，且扩充时只能延长两条直角边中的一条，则扩充后等腰三角形绿地的面积为8或10或12或$\frac{25}{3}$或$\frac{15}{2}$m²．

Answer 1

分析 由于扩充所得的等腰三角形腰和底不确定，若设扩充所得的三角形是△ABD，则应分为①BC=CD，②AC=CD，③AD=BD，④AB=BD，⑤AD=AB，5种情况进行讨论．

解答 解：①如图1：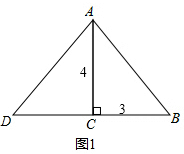

当BC=CD=3m时；
由于AC⊥BD，则AB=AD=5m；
此时等腰三角形绿地的面积：$\frac{1}{2}$×6×4=12（m²）；

②如图2：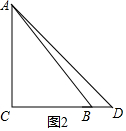

当AC=CD=4m时；
∵AC⊥CB，
此时等腰三角形绿地的面积：$\frac{1}{2}$×4×4=8（m²）；

③图3：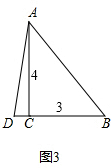

当AD=BD时，设AD=BD=xm；
Rt△ACD中，BD=xm，CD=（x-3）m；
由勾股定理，得AD²=DC²+CA²，即（x-3）²+4²=x²，
解得x=$\frac{25}{6}$；
此时等腰三角形绿地的面积：$\frac{1}{2}$×BD×AC=$\frac{1}{2}$×$\frac{25}{6}$×4=$\frac{25}{3}$（m²）．

④如图4，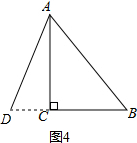

延长BC到D使BD等于5m，
此时AB=BD=5m，
故CD=2m，
$\frac{1}{2}$•BD•AC=$\frac{1}{2}$×5×4=10（m²）．

⑤如图5，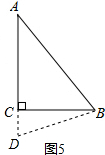

延长AC到D使AD等于5m，
此时AB=AD=5m，
故BC=3m，
$\frac{1}{2}$•BC•AD=$\frac{1}{2}$×5×3=$\frac{15}{2}$（m²）．
故答案为：8或10或12或$\frac{25}{3}$或$\frac{15}{2}$．

点评 此题主要考查了等腰三角形的性质以及勾股定理的应用，解决问题的关键是根据题意正确画出图形．