题目内容
13. 如图,在△ABC中,AB=AC,∠A=36°,BD是△ABC的角平分线,则∠ABD=36°.
如图,在△ABC中,AB=AC,∠A=36°,BD是△ABC的角平分线,则∠ABD=36°.
分析 由已知根据等腰三角形的性质易得两底角的度数,结合角平分线的性质和三角形内角和定理即可求解.
解答 解:∵AB=AC,∠A=36°,
∴∠ABC=∠C=(180°-36°)÷2=72°,
又∵BD为∠ABC的平分线,
∴∠ABD=36°,
故答案为:36
点评 本题考查了三角形内角和定理及等腰三角形的性质、角平分线的性质;综合运用各种知识是解答本题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
3.若抛物线y=x2-2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移一个单位,再沿铅直方向向上平移三个单位,则原抛物线图象的解析式应变为( )
| A. | y=(x-2)2+3 | B. | y=(x-2)2+5 | C. | y=x2-1 | D. | y=x2+4 |
18. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.当甲、乙两车相距50千米时,时间t的值最多有( )
甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.当甲、乙两车相距50千米时,时间t的值最多有( )
 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.当甲、乙两车相距50千米时,时间t的值最多有( )
甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.当甲、乙两车相距50千米时,时间t的值最多有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.下列计算正确的是( )
| A. | (-2)3=8 | B. | $\sqrt{4}$=±2 | C. | $\root{3}{-8}$=-2 | D. | |-2|=-2 |
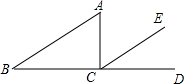 如图,点B、C、D在同一条直线上,CE∥AB,∠ACB=90°,如果∠ECD=36°,那么∠A﹦54°.
如图,点B、C、D在同一条直线上,CE∥AB,∠ACB=90°,如果∠ECD=36°,那么∠A﹦54°.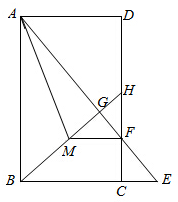 如图所示,在矩形ABCD中,点E是边BC延长线上一点,连结AE,交DC于点F,作BH⊥AE于点G,交DC于点H,作FM∥BC交BH于点M,连结AM.且FH=FE.AD=2$\sqrt{7}$.AG=6.
如图所示,在矩形ABCD中,点E是边BC延长线上一点,连结AE,交DC于点F,作BH⊥AE于点G,交DC于点H,作FM∥BC交BH于点M,连结AM.且FH=FE.AD=2$\sqrt{7}$.AG=6.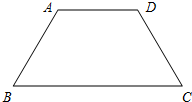 如图,在梯形ABCD中,AD∥BC,若AB=AD=DC=2,∠A=120°,则梯形ABCD的周长为10.
如图,在梯形ABCD中,AD∥BC,若AB=AD=DC=2,∠A=120°,则梯形ABCD的周长为10.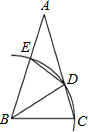 △ABC中,AB=AC,∠A=30°,以B为圆心,BC长为半径画弧,分别交AC,AB于D,E两点,并连结BD,DE. 则∠BDE的度数为67.5°.
△ABC中,AB=AC,∠A=30°,以B为圆心,BC长为半径画弧,分别交AC,AB于D,E两点,并连结BD,DE. 则∠BDE的度数为67.5°.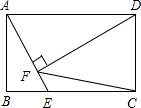 如图,在矩形ABCD中,AB=2$\sqrt{2}$,AD=4,点E是BC边上一个动点,连接AE,作DF⊥AE于点F,当BE的长为2或2$\sqrt{2}$或4-2$\sqrt{2}$时,△CDF是等腰三角形.
如图,在矩形ABCD中,AB=2$\sqrt{2}$,AD=4,点E是BC边上一个动点,连接AE,作DF⊥AE于点F,当BE的长为2或2$\sqrt{2}$或4-2$\sqrt{2}$时,△CDF是等腰三角形.