题目内容
18. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.当甲、乙两车相距50千米时,时间t的值最多有( )
甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.当甲、乙两车相距50千米时,时间t的值最多有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由图象所给数据可求得甲、乙两车离开A城的距离y与时间t的关系式,再令两函数解析式的差为50,可求得t,即可得出答案.
解答 解:设甲车离开A城的距离y与t的关系式为y甲=kt,
把(5,300)代入可求得k=60,则y甲=60t.
设乙车离开A城的距离y与t的关系式为y乙=mt+n,
把(1,0)和(4,300)代入可得
$\left\{\begin{array}{l}{m+n=0}\\{4m+n=300}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=100}\\{n=-100}\end{array}\right.$,
所以y乙=100t-100.
令|y甲-y乙|=50,
可得|60t-100t+100|=50,即|100-40t|=50,
当100-40t=50时,可解得t=$\frac{5}{4}$,
当100-40t=-50时,可解得t=$\frac{15}{4}$,
又当t=$\frac{5}{6}$时,y甲=50,此时乙还没出发,
当t=$\frac{25}{6}$时,乙到达B城,y甲=250;
综上可知当t的值为$\frac{5}{4}$或$\frac{15}{4}$或$\frac{5}{6}$或$\frac{25}{6}$时,两车相距50千米.
故选D.
点评 本题主要考查一次函数的应用,掌握一次函数图象的意义是解题的关键,特别注意t是甲车所用的时间.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.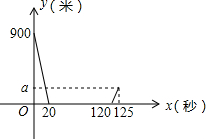 设甲、乙两车在同一直线公路上相向匀速行驶,相遇后两车停下来,把乙车的货物卸到甲车用了100秒,然后两车分别按原路原速返回.设x秒后两车之间的距离为y米,y关于x的函数关系如图所示,则a=225米.
设甲、乙两车在同一直线公路上相向匀速行驶,相遇后两车停下来,把乙车的货物卸到甲车用了100秒,然后两车分别按原路原速返回.设x秒后两车之间的距离为y米,y关于x的函数关系如图所示,则a=225米.
 设甲、乙两车在同一直线公路上相向匀速行驶,相遇后两车停下来,把乙车的货物卸到甲车用了100秒,然后两车分别按原路原速返回.设x秒后两车之间的距离为y米,y关于x的函数关系如图所示,则a=225米.
设甲、乙两车在同一直线公路上相向匀速行驶,相遇后两车停下来,把乙车的货物卸到甲车用了100秒,然后两车分别按原路原速返回.设x秒后两车之间的距离为y米,y关于x的函数关系如图所示,则a=225米.
7.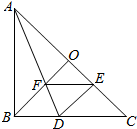 如图,在Rt△ABC中,AB=CB,BO⊥AC,DA平分∠BAC,DE⊥AC,连接EF,下列结论:①tan∠ADB=2;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点D不一定落在AC上;④BD=BF;⑤S四边形DFOE=S△AOF,上述结论中正确的个数是( )
如图,在Rt△ABC中,AB=CB,BO⊥AC,DA平分∠BAC,DE⊥AC,连接EF,下列结论:①tan∠ADB=2;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点D不一定落在AC上;④BD=BF;⑤S四边形DFOE=S△AOF,上述结论中正确的个数是( )
 如图,在Rt△ABC中,AB=CB,BO⊥AC,DA平分∠BAC,DE⊥AC,连接EF,下列结论:①tan∠ADB=2;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点D不一定落在AC上;④BD=BF;⑤S四边形DFOE=S△AOF,上述结论中正确的个数是( )
如图,在Rt△ABC中,AB=CB,BO⊥AC,DA平分∠BAC,DE⊥AC,连接EF,下列结论:①tan∠ADB=2;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点D不一定落在AC上;④BD=BF;⑤S四边形DFOE=S△AOF,上述结论中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8. 如图,沿箭头所指的方向看一个正三棱柱,它的三视图应该是( )
如图,沿箭头所指的方向看一个正三棱柱,它的三视图应该是( )
 如图,沿箭头所指的方向看一个正三棱柱,它的三视图应该是( )
如图,沿箭头所指的方向看一个正三棱柱,它的三视图应该是( )| A. |  | B. |  | C. |  | D. |  |
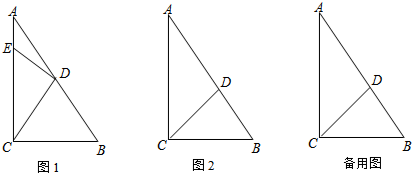
 如图,在△ABC中,AB=AC,∠A=36°,BD是△ABC的角平分线,则∠ABD=36°.
如图,在△ABC中,AB=AC,∠A=36°,BD是△ABC的角平分线,则∠ABD=36°.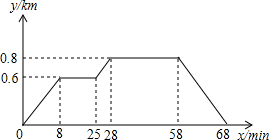 已知小明家、食堂、图书馆在同一直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.如图反映了这个过程中,小明离家的距离y与时间x之间的对应关系,根据图象可得,当25≤x≤28时,y与x的函数关系式是y=$\frac{1}{15}$x-$\frac{16}{15}$.
已知小明家、食堂、图书馆在同一直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.如图反映了这个过程中,小明离家的距离y与时间x之间的对应关系,根据图象可得,当25≤x≤28时,y与x的函数关系式是y=$\frac{1}{15}$x-$\frac{16}{15}$.