题目内容
2.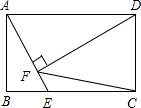 如图,在矩形ABCD中,AB=2$\sqrt{2}$,AD=4,点E是BC边上一个动点,连接AE,作DF⊥AE于点F,当BE的长为2或2$\sqrt{2}$或4-2$\sqrt{2}$时,△CDF是等腰三角形.
如图,在矩形ABCD中,AB=2$\sqrt{2}$,AD=4,点E是BC边上一个动点,连接AE,作DF⊥AE于点F,当BE的长为2或2$\sqrt{2}$或4-2$\sqrt{2}$时,△CDF是等腰三角形.
分析 过点C作CM⊥DF,垂足为点M,判断△CDF是等腰三角形,要分类讨论,①CF=CD;②DF=DC;③FD=FC,根据相似三角形的性质进行求解.
解答 解:①CF=CD时,过点C作CM⊥DF,垂足为点M,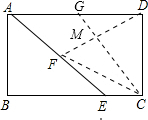
则CM∥AE,DM=MF,(1分)
延长CM交AD于点G,
∴AG=GD=2,
∴CE=2,
∴当BE=2时,△CDF是等腰三角形;
②DF=DC时,则DF=DC=AB=2$\sqrt{2}$,
∵DF⊥AE,AD=2,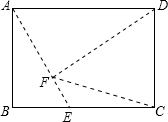
∴∠DAE=45°,
则BE=2$\sqrt{2}$,
∴当BE=2$\sqrt{2}$时,△CDF是等腰三角形;
③FD=FC时,则点F在CD的垂直平分线上,故F为AE中点.
∵AB=2$\sqrt{2}$,BE=x,
∴AE=$\sqrt{8+{x}^{2}}$,
AF=$\frac{\sqrt{8+{x}^{2}}}{2}$,
∵△ADF∽△EAB,
∴$\frac{AD}{AE}=\frac{AF}{EB}$,即$\frac{4}{\sqrt{8+{x}^{2}}}=\frac{\frac{\sqrt{8{+x}^{2}}}{2}}{x}$,
解得:x=4-2$\sqrt{2}$或x=4+2$\sqrt{2}$(舍去)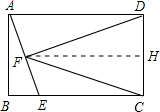 ;
;
∴当BE=4-2$\sqrt{2}$时,△CDF是等腰三角形.
综上,当BE=2或2$\sqrt{2}$或4-2$\sqrt{2}$ 时,△CDF是等腰三角形.
故答案为:2或2$\sqrt{2}$或4-2$\sqrt{2}$.
点评 此题难度比较大,主要考查矩形的性质、相似三角形的性质及等腰三角形的判定,考查知识点比较多,综合性比较强,另外要注意辅助线的作法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.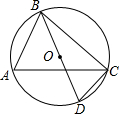 如图,⊙O的直径BD=6,∠A=60°,则BC的长度为( )
如图,⊙O的直径BD=6,∠A=60°,则BC的长度为( )
 如图,⊙O的直径BD=6,∠A=60°,则BC的长度为( )
如图,⊙O的直径BD=6,∠A=60°,则BC的长度为( )| A. | $\sqrt{3}$ | B. | 3 | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
7.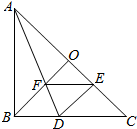 如图,在Rt△ABC中,AB=CB,BO⊥AC,DA平分∠BAC,DE⊥AC,连接EF,下列结论:①tan∠ADB=2;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点D不一定落在AC上;④BD=BF;⑤S四边形DFOE=S△AOF,上述结论中正确的个数是( )
如图,在Rt△ABC中,AB=CB,BO⊥AC,DA平分∠BAC,DE⊥AC,连接EF,下列结论:①tan∠ADB=2;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点D不一定落在AC上;④BD=BF;⑤S四边形DFOE=S△AOF,上述结论中正确的个数是( )
 如图,在Rt△ABC中,AB=CB,BO⊥AC,DA平分∠BAC,DE⊥AC,连接EF,下列结论:①tan∠ADB=2;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点D不一定落在AC上;④BD=BF;⑤S四边形DFOE=S△AOF,上述结论中正确的个数是( )
如图,在Rt△ABC中,AB=CB,BO⊥AC,DA平分∠BAC,DE⊥AC,连接EF,下列结论:①tan∠ADB=2;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点D不一定落在AC上;④BD=BF;⑤S四边形DFOE=S△AOF,上述结论中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.某网上电器商城销售某种品牌的高端电器.已知该电器按批发价上浮50%进行标价,若按照标价的九折销售,则可获纯利润350元,现由于商城搞促销,该电器按照标价的八折销售,则可获纯利润( )
| A. | 180元 | B. | 200元 | C. | 220元 | D. | 240元 |
11.天然气公司为了解某社区居民使用天然气的情况,随机对该社区10户居民进行了调查,如表是这10户居民2016年3月份用气量的调查结果:
则这10户居民月用气量(单位:立方米)的中位数是( )
| 居民户数 | 1 | 2 | 3 | 4 |
| 月用气量(立方米) | 14 | 15 | 22 | 25 |
| A. | 14 | B. | 15 | C. | 22 | D. | 25 |
12.百合花的花粉的直径约0.000000087米,这里0.000000087用科学记数法表示为( )
| A. | 8.7×10-7 | B. | 8.7×10-8 | C. | 8.7×10-9 | D. | 0.87×10-8 |
 如图,在△ABC中,AB=AC,∠A=36°,BD是△ABC的角平分线,则∠ABD=36°.
如图,在△ABC中,AB=AC,∠A=36°,BD是△ABC的角平分线,则∠ABD=36°.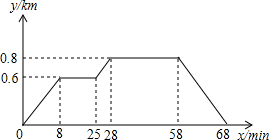 已知小明家、食堂、图书馆在同一直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.如图反映了这个过程中,小明离家的距离y与时间x之间的对应关系,根据图象可得,当25≤x≤28时,y与x的函数关系式是y=$\frac{1}{15}$x-$\frac{16}{15}$.
已知小明家、食堂、图书馆在同一直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.如图反映了这个过程中,小明离家的距离y与时间x之间的对应关系,根据图象可得,当25≤x≤28时,y与x的函数关系式是y=$\frac{1}{15}$x-$\frac{16}{15}$.