题目内容
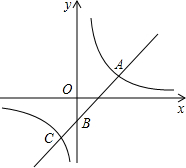 如图,在平面直角坐标系xOy中,反比例函数y=
如图,在平面直角坐标系xOy中,反比例函数y=| a |
| x |
(1)求反比例函数和一次函数的解析式;
(2)直接写出当x为何值时,kx+b-
| a |
| x |
(3)设直线AC与y轴交于点B,若P是坐标轴上一点,且满足△PAB的面积是6,求点P的坐标.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把C点的坐标代入反比例函数解析式可求得a,把A点坐标代入可求得m,可得到A点坐标,再把A、C坐标代入一次函数解析式可求得k、b的值,可求得两函数的解析式;
(2)根据A、C两点的坐标,结合函数图象可直接得到不等式的解集;
(3)分P点在x轴和y轴上,分别设出P点坐标,根据条件可得到关于坐标的方程,可求得P点的坐标.
(2)根据A、C两点的坐标,结合函数图象可直接得到不等式的解集;
(3)分P点在x轴和y轴上,分别设出P点坐标,根据条件可得到关于坐标的方程,可求得P点的坐标.
解答:解:(1)∵函数y=
的图象过A、C两点,
∴a=-2×(-3)=2m,解得a=6,m=3,
∴反比例函数解析式为y=
,A点坐标为(3,2),
又∵一次函数y=kx+b过A、C两点,
∴把A、C坐标代入可得
,解得
,
∴一次函数解析式为y=x-1;
(2)∵kx+b-
>0可化为kx+b>
,
∴对应x的范围为满足一次函数值大于反比例函数值的x的范围,
∴x的范围为x>3或-2<x<0;
(3)设一次函数与x轴交于D点,
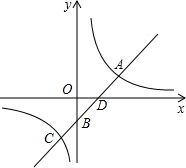
在y=x-1中,令x=0得y=-1,令y=0可得x=1,
∴B点坐标为(0,-1),D点坐标为(1,0),
当P点在x轴上时,设P为(x,0),
则PD=|x-1|,由A(3,2),B(0,-1)可得A、B两点到x轴的距离分别为2、1,
∴S△PAB=
×(2+1)×|x-1|=6,
解得x=5或-3,此时P点坐标为(5,0)或(-3,0);
当P点在y轴上时,设P为(0,y),
则PB=|y+1|,由A(3,2),可得A点到y轴的距离为3,
∴S△PAB=
×|y+1|×3=6,
解得y=3或-5,此时P点坐标为(0,3)或(0,-5),
综上可知P点坐标为(5,0)或(-3,0)或(0,3)或(0,-5).
| a |
| x |
∴a=-2×(-3)=2m,解得a=6,m=3,
∴反比例函数解析式为y=
| 6 |
| x |
又∵一次函数y=kx+b过A、C两点,
∴把A、C坐标代入可得
|
|
∴一次函数解析式为y=x-1;
(2)∵kx+b-
| a |
| x |
| a |
| x |
∴对应x的范围为满足一次函数值大于反比例函数值的x的范围,
∴x的范围为x>3或-2<x<0;
(3)设一次函数与x轴交于D点,

在y=x-1中,令x=0得y=-1,令y=0可得x=1,
∴B点坐标为(0,-1),D点坐标为(1,0),
当P点在x轴上时,设P为(x,0),
则PD=|x-1|,由A(3,2),B(0,-1)可得A、B两点到x轴的距离分别为2、1,
∴S△PAB=
| 1 |
| 2 |
解得x=5或-3,此时P点坐标为(5,0)或(-3,0);
当P点在y轴上时,设P为(0,y),
则PB=|y+1|,由A(3,2),可得A点到y轴的距离为3,
∴S△PAB=
| 1 |
| 2 |
解得y=3或-5,此时P点坐标为(0,3)或(0,-5),
综上可知P点坐标为(5,0)或(-3,0)或(0,3)或(0,-5).
点评:本题主要考查待定系数法求函数解析式和函数的交点问题,掌握函数图象的交点坐标满足两函数解析式是解题的关键.注意分类讨论思想、数形结合思想的应用.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 如图,是一个正方体的展开图,正方体的每个面都有一个数字,只有一对相对两面的数字的积是有理数,这个有理数是( )
如图,是一个正方体的展开图,正方体的每个面都有一个数字,只有一对相对两面的数字的积是有理数,这个有理数是( )| A、4 | B、6 | C、9 | D、10 |
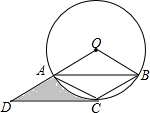 如图,⊙O是△ABC的外接圆,AC=BC,CD∥AB交OA的延长线于点D.
如图,⊙O是△ABC的外接圆,AC=BC,CD∥AB交OA的延长线于点D.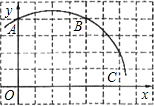 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.若A点的坐标为(0,4),D点的坐标为(7,0).
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.若A点的坐标为(0,4),D点的坐标为(7,0).