题目内容
15.计算(1)分解因式
2x3-8x
(x2+1)2-4x2
(2)解分式方程:$\frac{1}{x-1}$+$\frac{2x}{x+1}$=2.
分析 (1)原式提取公因式,再利用平方差公式分解即可;原式利用平方差公式及完全平方公式分解即可;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=2x(x2-4)=2x(x+2)(x-2);原式=(x2+1+2x)(x2+1-2x)=(x+1)2(x-1)2;
(2)去分母得:x+1+2x2-2x=2x2-2,
解得:x=3,
经检验x=3是分式方程的解.
点评 此题考查了提公因式法与公式法的综合运用,以及解分式方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
20.若代数式$\frac{{\sqrt{x+5}}}{x-1}$有意义,则x应满足( )
| A. | x=0 | B. | x≠1 | C. | x≥-5 | D. | x≥-5且x≠1 |
7.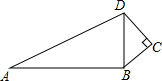 如图,己知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°,则AD=( )
如图,己知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°,则AD=( )
 如图,己知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°,则AD=( )
如图,己知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°,则AD=( )| A. | 10 | B. | 13 | C. | 8 | D. | 11 |
 已知直线y=$\frac{3}{4}$x+3与x轴相交于点A,与y轴相交于点B,P是直线AB上的一个动点,过P点分别作x轴、y轴的垂线PE,PF,如图所示,
已知直线y=$\frac{3}{4}$x+3与x轴相交于点A,与y轴相交于点B,P是直线AB上的一个动点,过P点分别作x轴、y轴的垂线PE,PF,如图所示,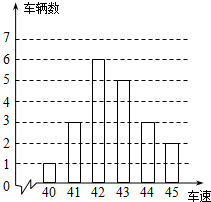 如图是交警在某个路口统计的某时段来往车辆的车速情况.(单位:千米/时).
如图是交警在某个路口统计的某时段来往车辆的车速情况.(单位:千米/时).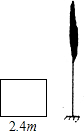 国旗法对国旗的构成由明确的规定,国旗应为长方形,长与宽的比为3:2,某学校所使用的国旗正是按这一比例制作的,长为2.4m.已知学校的旗杆高为10m,在无风的天气里,国旗会自然下垂,求国旗下垂时最低处离地面的距离是多少?(结果保留一位小数,$\sqrt{13}$≈3.6)
国旗法对国旗的构成由明确的规定,国旗应为长方形,长与宽的比为3:2,某学校所使用的国旗正是按这一比例制作的,长为2.4m.已知学校的旗杆高为10m,在无风的天气里,国旗会自然下垂,求国旗下垂时最低处离地面的距离是多少?(结果保留一位小数,$\sqrt{13}$≈3.6) 将一列数$-1,\frac{1}{2},-\frac{1}{3},\frac{1}{4},-\frac{1}{5},\frac{1}{6},…$按一定的规律排,如右表.按此规律排下去,第200行第100个数为$\frac{1}{20200}$.
将一列数$-1,\frac{1}{2},-\frac{1}{3},\frac{1}{4},-\frac{1}{5},\frac{1}{6},…$按一定的规律排,如右表.按此规律排下去,第200行第100个数为$\frac{1}{20200}$.