题目内容
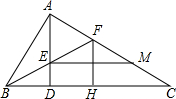 已知,△ABC中,∠BAC=90°,AD是高,BF平分∠ABC交AD于点E,交AC于F,作FH⊥BC,EM∥BC,写出图中所有与AF相等的线段,并证明.
已知,△ABC中,∠BAC=90°,AD是高,BF平分∠ABC交AD于点E,交AC于F,作FH⊥BC,EM∥BC,写出图中所有与AF相等的线段,并证明.考点:全等三角形的判定与性质,角平分线的性质
专题:
分析:AF=AE=FH=MC.由△ABC中,∠BAC=90°,AD⊥BC与FB平分∠ABC,根据等角的余角相等,易得∠AFE=∠BED,又由对顶角相等,可得∠AEF=∠AFE,则可证得AE=AF.然后利用全等三角形(Rt△AEM≌Rt△FHC)来证得AM=FC,AF=MC.
解答:
解:AF=AE=FH=MC.理由如下:
∵△ABC中,∠BAC=90°,
∴∠ABF+∠AFB=90°,
∵AD⊥BC,
∴∠ADB=90°,
∴∠EBD+∠BED=90°,
∵FB平分∠ABC,
∴∠ABF=∠EBD,
∴∠BED=∠AFE,
∵∠BED=∠AEF,
∴∠AEF=∠AFE,
∴AE=AF.
∵点F在∠ABC的角平分线上,
∴AF=FH.
∵AE=AE,AF=FH,
∴AE=FH.
易证 Rt△AEM≌Rt△FHC,
∴AM=FC,
∴AF=MC.
∵△ABC中,∠BAC=90°,
∴∠ABF+∠AFB=90°,
∵AD⊥BC,
∴∠ADB=90°,
∴∠EBD+∠BED=90°,
∵FB平分∠ABC,
∴∠ABF=∠EBD,
∴∠BED=∠AFE,
∵∠BED=∠AEF,
∴∠AEF=∠AFE,

∴AE=AF.
∵点F在∠ABC的角平分线上,
∴AF=FH.
∵AE=AE,AF=FH,
∴AE=FH.
易证 Rt△AEM≌Rt△FHC,
∴AM=FC,
∴AF=MC.
点评:此题考查了等腰三角形的判定,直角三角形的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在下列实数中,无理数是( )
A、-
| |||
| B、3.14 | |||
C、
| |||
D、
|
某种生物细胞的直径是0.000000012cm,用科学记数法表示这个数,正确的是( )
| A、12×10-7cm |
| B、1.2×10-7cm |
| C、12×10-8cm |
| D、1.2×10-8cm |
 如图,线段AB=DE,点C为线段AE的中点,下列式子中不正确的是( )
如图,线段AB=DE,点C为线段AE的中点,下列式子中不正确的是( )| A、BC=CD |
| B、CD=AC-AB |
| C、CD=AD-CE |
| D、CD=DE |
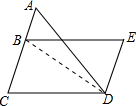 如图所示,BC=DE,BE=DC,求证:(1)BC∥DE;(2)∠A=∠ADE.小明是这样想的,请你给小明的每个想法填上依据.连结BD,在△BCD和△DEB中,
如图所示,BC=DE,BE=DC,求证:(1)BC∥DE;(2)∠A=∠ADE.小明是这样想的,请你给小明的每个想法填上依据.连结BD,在△BCD和△DEB中, 如图,已知AB∥CD,AE∥CF,BF=DE
如图,已知AB∥CD,AE∥CF,BF=DE