题目内容
 如图,已知AB∥CD,AE∥CF,BF=DE
如图,已知AB∥CD,AE∥CF,BF=DE求证:AB=CD.
考点:全等三角形的判定与性质
专题:证明题
分析:由平行可得∠B=∠D,∠AEF=∠CFE,可求得∠AEB=∠CFD,又结合条件可得BE=DF,可证明△ABE≌△CDF,可得AB=CD.
解答:
证明:
∵AB∥CD,
∴∠B=∠D,
∵AE∥CF,
∴∠AEF=∠CFE,
∴∠AEB=∠CFD,
∵BF=DE,
∴BF-EF=DE-EF,即BE=DF,
在△ABE和△CDF中
∴△ABE≌△CDF(ASA),
∴AB=CD.
∵AB∥CD,
∴∠B=∠D,
∵AE∥CF,
∴∠AEF=∠CFE,
∴∠AEB=∠CFD,
∵BF=DE,
∴BF-EF=DE-EF,即BE=DF,
在△ABE和△CDF中
|
∴△ABE≌△CDF(ASA),
∴AB=CD.
点评:本题主要考查全等三角的判定和性质,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
相关题目
 观察下图,在A、B、C、D四幅图案中,能通过图案平移得到的是( )
观察下图,在A、B、C、D四幅图案中,能通过图案平移得到的是( )A、 |
B、 |
C、 |
D、 |
若( )×(-2)=1,则括号内填一个实数应该是( )
A、-
| ||
| B、2 | ||
| C、-2 | ||
D、
|
下列方程变形错误的是( )
A、由方程
| ||||
B、由方程
| ||||
C、由方程
| ||||
D、由方程x-
|
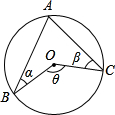 如图,AB,AC是O的两条弦,圆心O在∠BAC的内部,若∠ABO=α,∠ACO=β,∠BOC=θ,则下列关系式中,正确的是( )
如图,AB,AC是O的两条弦,圆心O在∠BAC的内部,若∠ABO=α,∠ACO=β,∠BOC=θ,则下列关系式中,正确的是( )| A、θ=α+β |
| B、θ+α+β=360° |
| C、θ+α+β=180° |
| D、θ=2α+2β |
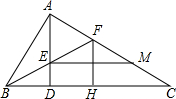 已知,△ABC中,∠BAC=90°,AD是高,BF平分∠ABC交AD于点E,交AC于F,作FH⊥BC,EM∥BC,写出图中所有与AF相等的线段,并证明.
已知,△ABC中,∠BAC=90°,AD是高,BF平分∠ABC交AD于点E,交AC于F,作FH⊥BC,EM∥BC,写出图中所有与AF相等的线段,并证明.
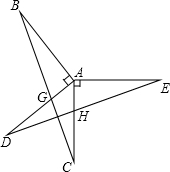 如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H.
如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H.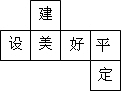 2015年,县委、县政府做出了“小微企业富民,大中企业强县,唱响千年文化,建设美好平定”的决策,如图是小明制作的一个正方体的表面展开图,原正方体中与“建”字所在的面相对的面上标的字是( )
2015年,县委、县政府做出了“小微企业富民,大中企业强县,唱响千年文化,建设美好平定”的决策,如图是小明制作的一个正方体的表面展开图,原正方体中与“建”字所在的面相对的面上标的字是( )