题目内容
14.某超市用5 000元购进一批新品种的苹果进行试销,由于销售状况良好,超市又调拨11 000元资金购进该品种苹果,但这次的进货价比试销时每千克多了0.5元,购进苹果数量是试销时的2倍.(1)试销时该品种苹果的进货价是每千克多少元?
(2)如果超市将该品种苹果按每千克7元的定价出售,当大部分苹果售出后,余下的苹果定价为4元,超市在这两次苹果销售中的盈利不低于4 100元,那么余下的苹果最多多少千克?
分析 (1)设试销时该品种苹果的进货价是每千克x元,则实际进货价为(0.5+x)元,根据这次购进苹果数量是试销时的2倍,列方程求解;
(2)设余下的苹果为y千克,求出总购进的苹果数量,根据超市在这两次苹果销售中的盈利不低于4 100元,列不等式求解.
解答 解:(1)设试销时该品种苹果的进货价是每千克x元,则实际进货价为(0.5+x)元,
由题意得,$\frac{5000}{x}$×2=$\frac{11000}{x+0.5}$,
解得:x=5,
经检验,x=5是原分式方程的解,且符合题意,
答:试销时该品种苹果的进货价是每千克5元;
(2)由(1)得,总共购进苹果:5000÷5×3=3000(kg),
设余下的苹果为y千克,
由题意得,7(3000-y)+4y-5000-11000≥4 100,
解得:y≤300.
答:余下的苹果最多为300千克.
点评 本题考查了一元一次不等式和分式方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解,注意检验.

练习册系列答案
相关题目
5.小明同学在期中考试中,数学、语文的平均分是95分,而数学、语文、英语三科平均分不低于98分,则小明同学的英语成绩至少为( )
| A. | 96分 | B. | 98分 | C. | 100分 | D. | 104分 |
19.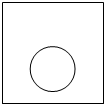 如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )
如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )
 如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )
如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )| A. | πr2 | B. | a2-πr2 | C. | 4r2-πr2 | D. | $\frac{a^2}{4}$ |
 如图,三角形DEF是由三角形ABC通过平移得到,且点B,E,C,F在同一条直线上,若BF=14,EC=6,则BE的长度是4.
如图,三角形DEF是由三角形ABC通过平移得到,且点B,E,C,F在同一条直线上,若BF=14,EC=6,则BE的长度是4.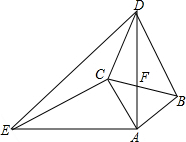 如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.
如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.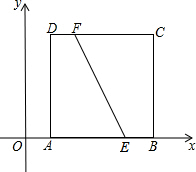 如图,在平面直角坐标系中,正方形ABCD的顶点,A、B、C的坐标分别为(1,0)、(5,0)、(5,4),点E、F的坐标分别为(4,0)、(2,4),过EF的中点作直线,若此直线被正方形的两边所截得的线段的长与线段EF的长相等,则这条线段靠近点A的端点的坐标为(1,1)、(1,3)、(2,0).
如图,在平面直角坐标系中,正方形ABCD的顶点,A、B、C的坐标分别为(1,0)、(5,0)、(5,4),点E、F的坐标分别为(4,0)、(2,4),过EF的中点作直线,若此直线被正方形的两边所截得的线段的长与线段EF的长相等,则这条线段靠近点A的端点的坐标为(1,1)、(1,3)、(2,0).