题目内容
6.下列根据等式的性质变形正确的有( )①若a=b,则ac=bc;
②若ac=bc,则a=b;
③若a=b,则$\frac{a}{c}$=$\frac{b}{c}$;
④若$\frac{a}{c}$=$\frac{b}{c}$,则a=b;
⑤若a=b,则$\frac{a}{{c}^{2}+1}$=$\frac{b}{{c}^{2}+1}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用等式的性质进行解答并作出判断.
解答 解:①在等式a=b的两边同时乘以c,等式仍成立,即ac=bc,故正确;
②当c=0时,a=b不一定成立,故错误;
③若c=0时,$\frac{a}{c}$=$\frac{b}{c}$不一定成立,故错误;
④等式$\frac{a}{c}$=$\frac{b}{c}$的两边同时乘以c,等式仍成立,即a=b,故正确;
⑤因为c2+1>0,所以在等式a=b的两边同时除以(c2+1),等式仍成立,即$\frac{a}{{c}^{2}+1}$=$\frac{b}{{c}^{2}+1}$,故正确.
综上所述,正确的结论有3个.
故选:C.
点评 本题主要考查了等式的基本性质.
等式性质:1、等式的两边同时加上或减去同一个数或字母,等式仍成立;
2、等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.

练习册系列答案
相关题目
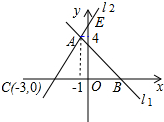 如图,直线l1的解析式是y=-x+3,与直线l2交于点A,且两直线分别交x轴于点B,C,交y轴于点D,E.
如图,直线l1的解析式是y=-x+3,与直线l2交于点A,且两直线分别交x轴于点B,C,交y轴于点D,E.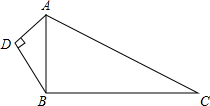 如图,已知AD=6,BD=8,AC=26,BC=24,∠ADB=90°.问△ABC是直角三角形吗?并说明理由.
如图,已知AD=6,BD=8,AC=26,BC=24,∠ADB=90°.问△ABC是直角三角形吗?并说明理由.