题目内容
11.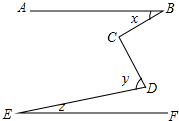 如图,已知AB∥EF,∠C=90°,求证:x+y-z=90°.
如图,已知AB∥EF,∠C=90°,求证:x+y-z=90°.
分析 过C作CM∥AB,延长CD交EF于N,根据三角形外角性质求出∠CNE=y-z,根据平行线性质得出∠1=x,∠2=∠CNE,代入求出即可.
解答  证明:过C作CM∥AB,延长CD交EF于N,则∠CDE=∠E+∠CNE,即∠CNE=y-z
证明:过C作CM∥AB,延长CD交EF于N,则∠CDE=∠E+∠CNE,即∠CNE=y-z
∵CM∥AB,AB∥EF,
∴CM∥AB∥EF,
∴∠ABC=x=∠1,∠2=∠CNE,
∵∠BCD=90°,
∴∠1+∠2=90°,
∴x+y-z=90°.
点评 本题考查了平行线的性质和三角形外角性质的应用,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,题目比较好,难度适中.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
2.抛物线y=ax2经过点(1,3),则a的值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 9 |
3.二次函数y=ax2+bx+c(a,b,c为常数,a≠0)中,x与y的部分对应值如下表:
有下列结论:
①函数有最大值,且最大值为1;
②若x0满足y=ax02+bx+c,则2<x0<3或-1<x0<0;
③若方程ax2+bx+c+m=0有两个不等的实数根且m<-1;
④对于任意实数m,当m≠1时,有m(am+b)<$\frac{1}{2}$.
其中正确结论的个数是( )
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | -3.5 | -1 | 0.5 | 1 | 0.5 | -1 | -3.5 | … |
①函数有最大值,且最大值为1;
②若x0满足y=ax02+bx+c,则2<x0<3或-1<x0<0;
③若方程ax2+bx+c+m=0有两个不等的实数根且m<-1;
④对于任意实数m,当m≠1时,有m(am+b)<$\frac{1}{2}$.
其中正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
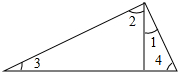 如图,已知∠1+∠2=90°,∠2+∠3=90°
如图,已知∠1+∠2=90°,∠2+∠3=90°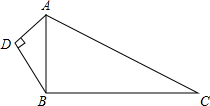 如图,已知AD=6,BD=8,AC=26,BC=24,∠ADB=90°.问△ABC是直角三角形吗?并说明理由.
如图,已知AD=6,BD=8,AC=26,BC=24,∠ADB=90°.问△ABC是直角三角形吗?并说明理由.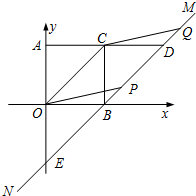 如图,在平面直角坐标系xOy内,?AOBC的顶点A、O、B、C的坐标分别为(0,1)、(0,0)、(1,0)、(1、1),过点B的直线MN与OC平行,AC的延长线交MN于点D,点P是直线MN上的一个动点,CQ∥OP交MN于点Q.
如图,在平面直角坐标系xOy内,?AOBC的顶点A、O、B、C的坐标分别为(0,1)、(0,0)、(1,0)、(1、1),过点B的直线MN与OC平行,AC的延长线交MN于点D,点P是直线MN上的一个动点,CQ∥OP交MN于点Q.