题目内容
6．用火柴棒按如图的方式搭三角形．第一个图形要3根火柴棒，第二个图形要5根火柴棒，那么第5个图形要11根火柴棒，第n个图形要2n+1根火柴棒，
分析 设第n个图形需要an（n为正整数）根火柴棒，根据给定图形找出部分an的值，根据数值的变化找出变化规律“an=2n+1”，依此规律即可得出结论．
解答 解：设第n个图形需要an（n为正整数）根火柴棒，
观察，发现规律：a1=3，a2=5，a3=7，a4=9，…，
∴an=2n+1．
当n=5时，a5=2×5+1=11．
故答案为：11；2n+1．
点评 本题考查了规律型中的图形的变化类，解题的关键是找出变化规律“an=2n+1”．本题属于基础题，难度不大，解决该题型题目时，根据给定图形中的数据找出变化规律是关键．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
如图，在正方形ABCD中，E为AB的中点，当$\frac{AF}{AD}$=$\frac{1}{3}$时，△AEF∽△BCE．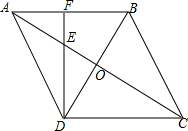
如图，在?ABCD中，对角线AC与BD相交于点O，∠CAB=∠ACB．