题目内容
12. 如图,在?ABCD中,AC,BD交于点O,AE⊥BC于E,EO交AD于F,求证:四边形AECF是矩形.
如图,在?ABCD中,AC,BD交于点O,AE⊥BC于E,EO交AD于F,求证:四边形AECF是矩形.
分析 由ASA证明△AOF≌△COE,得出对应边相等EO=FO,证出四边形AFCE为平行四边形,再由AE⊥BC求出∠AEC=90°,根据矩形的判定得出即可.
解答 证明:∵四边形ABCD是矩形,
∴AE∥FC,
∴∠EAO=∠FCO,
∵EF垂直平分AC,
∴AO=CO,FE⊥AC,
在△AOF和△COE中,
$\left\{\begin{array}{l}{∠FAO=∠ECO}\\{AO=CO}\\{∠AOF=∠COE}\end{array}\right.$,
∴△AOF≌△COE(ASA),
∴EO=FO,
∵AO=OC,
∴四边形AFCE为平行四边形,
∵AE⊥BC,
∴∠AEC=90°,
∴四边形AFCE为矩形.
点评 本题考查了全等三角形的性质和判定平行四边形的判定和性质;熟练掌握矩形的判定,证明三角形全等是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.8的立方根是( )
| A. | 2 | B. | ±2 | C. | $2\sqrt{2}$ | D. | $±2\sqrt{2}$ |
7.一项工程,甲队独做需20天完成,乙队独做30天完成,若甲队独做8天,乙队再做3天,剩下的甲乙两队合做,还需几天完成?设还需x天完成,依题意可列方程( )
| A. | $\frac{8+x}{20}$+$\frac{3+x}{30}$=1 | B. | $\frac{x}{20}$+$\frac{x}{30}$=1 | C. | $\frac{8}{20}$+$\frac{3+x}{30}$=1 | D. | $\frac{8+x}{x}$+$\frac{3+x}{30}$=1 |
1. 如图,将矩形纸片ABCD折叠,使点B与点D重合,折痕为MN,若AB=2,BC=4,那么线段MN的长为( )
如图,将矩形纸片ABCD折叠,使点B与点D重合,折痕为MN,若AB=2,BC=4,那么线段MN的长为( )
 如图,将矩形纸片ABCD折叠,使点B与点D重合,折痕为MN,若AB=2,BC=4,那么线段MN的长为( )
如图,将矩形纸片ABCD折叠,使点B与点D重合,折痕为MN,若AB=2,BC=4,那么线段MN的长为( )| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\sqrt{5}$ | C. | $\frac{4\sqrt{5}}{5}$ | D. | 2$\sqrt{5}$ |
 甲、乙两地相距900km,一辆货车从甲地出发以60km∕h的速度开往乙地,另一辆轿车同时从乙地出发匀速开往甲地.图中的折线ABCD表示货车与轿车相距的距离y(km)与时间x(h)之间的函数图象,请根据图象,解答下列问题:
甲、乙两地相距900km,一辆货车从甲地出发以60km∕h的速度开往乙地,另一辆轿车同时从乙地出发匀速开往甲地.图中的折线ABCD表示货车与轿车相距的距离y(km)与时间x(h)之间的函数图象,请根据图象,解答下列问题: 如图,将一个正方形纸片AOCD,放置在平面直角坐标系中,点A(0,4),点O(0,0),点D在第一象限.点P为正方形AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点O落在点P处,点C落在点G处,PG交DC于点H,折痕为EF,连接OP,OH.设P点的横坐标为m.
如图,将一个正方形纸片AOCD,放置在平面直角坐标系中,点A(0,4),点O(0,0),点D在第一象限.点P为正方形AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点O落在点P处,点C落在点G处,PG交DC于点H,折痕为EF,连接OP,OH.设P点的横坐标为m. 如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上
如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上 如图,菱形ABCD中,AC=6,BD=8,则BC边上的高AE的长为4.8.
如图,菱形ABCD中,AC=6,BD=8,则BC边上的高AE的长为4.8.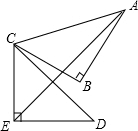 如图,在Rt△ABC中,∠B=90°,AB=BC=2,将△ABC绕点C顺时针旋转60°,得到△DEC,则AE的长是$\sqrt{2}$+$\sqrt{6}$.
如图,在Rt△ABC中,∠B=90°,AB=BC=2,将△ABC绕点C顺时针旋转60°,得到△DEC,则AE的长是$\sqrt{2}$+$\sqrt{6}$.