题目内容
将一个一元二次方程ax2+bx+c=0化为（x-m）2=
，则m为 ．
| b2-4ac |
| 4a2 |
考点：解一元二次方程-配方法
专题：
分析：方程两边同除以二次项系数，使二次项系数为1，并把常数项移到方程右边；方程两边同时加上一次项系数一半的平方；把左边配成一个完全平方式，右边化为一个常数．
解答：解：由ax2+bx+c=0，得
a（x2+
x）=-c，
a（x+
）2-
=-c，
（x+
）2=
，
所以 一个一元二次方程ax2+bx+c=0化为（x-m）2=
，则m为-
．
故答案是：-
．
a（x2+
| b |
| a |
a（x+
| b |
| 2a |
| b2 |
| 4a |
（x+
| b |
| 2a |
| b2-4ac |
| 4a2 |
所以 一个一元二次方程ax2+bx+c=0化为（x-m）2=
| b2-4ac |
| 4a2 |
| b |
| 2a |
故答案是：-
| b |
| 2a |
点评：本题考查了解一元二次方程--配方法．配方法的一般步骤：
（1）把常数项移到等号的右边；
（2）把二次项的系数化为1；
（3）等式两边同时加上一次项系数一半的平方．
选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．
（1）把常数项移到等号的右边；
（2）把二次项的系数化为1；
（3）等式两边同时加上一次项系数一半的平方．
选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．
练习册系列答案
阅读快车系列答案
相关题目
在△ABC中，AB=AC，∠BAC的平分线交BC于点D，过点B作BE∥AD交∠BAF的平分线于点E．
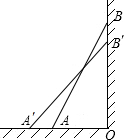如图，梯子AB靠在墙上，梯子的底端A到墙根O的距离为2m，梯子的顶端B到地面的距离为7m，现将梯子的底端A向外移动到A′，使梯子的底端A′到墙根O的距离等于3m，同时梯子的顶端B下降至B′，那么BB′（ ）| A、小于1m | B、大于1m |
| C、等于1m | D、小于或等于1m |