题目内容
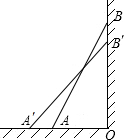如图，梯子AB靠在墙上，梯子的底端A到墙根O的距离为2m，梯子的顶端B到地面的距离为7m，现将梯子的底端A向外移动到A′，使梯子的底端A′到墙根O的距离等于3m，同时梯子的顶端B下降至B′，那么BB′（ ）| A、小于1m | B、大于1m |
| C、等于1m | D、小于或等于1m |
考点：勾股定理的应用
专题：
分析：由题意可知OA=2，OB=7，先利用勾股定理求出AB，梯子移动过程中长短不变，所以AB=A′B′，又由题意可知OA′=3，利用勾股定理分别求OB′长，把其相减得解．
解答：解：在直角三角形AOB中，因为OA=2，OB=7
由勾股定理得：AB=
，
由题意可知AB=A′B′=
，
又OA′=3，根据勾股定理得：OB′=
，
∴BB′=7-
＜1．
故选A．
由勾股定理得：AB=
| 53 |
由题意可知AB=A′B′=
| 53 |
又OA′=3，根据勾股定理得：OB′=
| 44 |
∴BB′=7-
| 44 |
故选A．
点评：本题考查了勾股定理的应用，属于基础题，解答本题的关键是掌握勾股定理的表达式．
练习册系列答案
相关题目
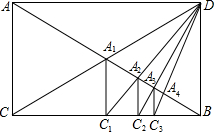如图，对于任意线段AB，可以构造以AB为对角线的矩形ACBD．连接CD，与AB交于A1点，过A1作BC的垂线段A1C1，垂足为C1；连接C1D，与AB交于A2点，过A2作BC的垂线段A2C2，垂足为C2；连接C2D，与AB交于A3点，过A3作BC的垂线段A3C3，垂足为C3…如此下去，可以依次得到点A4，A5，…，An．如果设AB的长为1，依次可求得A1B，A2B，A3B…的长，则AnB的长为（用n的代数式表示）（ ）如果满足∠ABC=60°，AC=12，BC=k的△ABC恰有一个，那么k的取值范围是（ ）
A、k=8
| ||
| B、0＜k≤12 | ||
| C、k≥12 | ||
D、0＜k≤12或k=8
|