题目内容
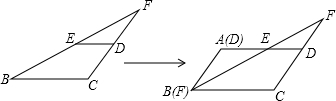
 在△ABC中,AB=AC,∠BAC的平分线交BC于点D,过点B作BE∥AD交∠BAF的平分线于点E.
在△ABC中,AB=AC,∠BAC的平分线交BC于点D,过点B作BE∥AD交∠BAF的平分线于点E.(1)求证:四边形ADBE是矩形;
(2)当∠BAC满足什么条件时,四边形ADBE是正方形.
考点:正方形的判定,矩形的判定
专题:
分析:(1)先根据AB=AC,AD平分∠BAC,得∠BAD=
∠BAC,AD⊥BC,然后根据AE是△ABC的外角平分线,可求出AD⊥AE,然后根据有一个角是直角的平行四边形是矩形得到四边形ADBE为矩形;
(2)根据矩形的性质可知当∠BAC=90°时,则∠ABC=∠BAD=45°,利用等腰三角形的性质定理可知对应边AD=BD,再运用邻边相等的矩形是正方形,问题得证.
| 1 |
| 2 |
(2)根据矩形的性质可知当∠BAC=90°时,则∠ABC=∠BAD=45°,利用等腰三角形的性质定理可知对应边AD=BD,再运用邻边相等的矩形是正方形,问题得证.
解答:(1) 证明:∵AB=AC,AD平分∠BAC,
证明:∵AB=AC,AD平分∠BAC,
∴∠BAD=
∠BAC,AD⊥BC,
∵AE是△ABC的外角平分线,
∴∠BAE=
∠BAF,
∵∠BAC+∠BAF=180°,
∴∠BAD+∠BAE=90°,即∠DAE=90°,
∴AD⊥AE,
∵AD⊥BC,
∴AE∥BC,
又∵BE∥AD,∠DAE=90°,
∴四边形ADBE是矩形;
(2)解:当∠BAC=90°时,四边形ADBE是正方形.理由如下:
∵AB=AC,AD平分∠BAC,∠BAC=90°,
∴∠ABC=∠C=∠BAD=∠CAD=45°,
∴AD=BD,
又∵四边形ADBE是矩形,
∴矩形ADBE为正方形.
 证明:∵AB=AC,AD平分∠BAC,
证明:∵AB=AC,AD平分∠BAC,∴∠BAD=
| 1 |
| 2 |
∵AE是△ABC的外角平分线,
∴∠BAE=
| 1 |
| 2 |
∵∠BAC+∠BAF=180°,
∴∠BAD+∠BAE=90°,即∠DAE=90°,
∴AD⊥AE,
∵AD⊥BC,
∴AE∥BC,
又∵BE∥AD,∠DAE=90°,
∴四边形ADBE是矩形;
(2)解:当∠BAC=90°时,四边形ADBE是正方形.理由如下:
∵AB=AC,AD平分∠BAC,∠BAC=90°,
∴∠ABC=∠C=∠BAD=∠CAD=45°,
∴AD=BD,
又∵四边形ADBE是矩形,
∴矩形ADBE为正方形.
点评:此题考查的是等腰三角形、矩形、正方形的判定与性质和三角形外角平分线的性质,具有一定的综合性,需要灵活应用.

练习册系列答案
相关题目