题目内容
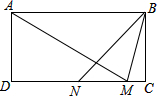 如图,在矩形ABCD中,AB=2BC,N为CD的中点,点M在CD上,且AM=AB,求∠MBN的度数.
如图,在矩形ABCD中,AB=2BC,N为CD的中点,点M在CD上,且AM=AB,求∠MBN的度数.考点:矩形的性质
专题:
分析:过点M作ME⊥AB于E,根据直角三角形30°角所对的直角边等于斜边的一半可得∠BAM=30°,再利用等腰三角形两底角相等求出∠ABM,然后求出∠CBM,再根据点N是CD的中点求出△BCM是等腰直角三角形,根据等腰直角三角形的性质求出∠CBN=45°,然后根据∠MBN=∠CBN-∠CBM代入数据计算即可得解.
解答: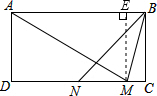 解:如图,过点M作ME⊥AB于E,则EM=BC,
解:如图,过点M作ME⊥AB于E,则EM=BC,
∵AB=2BC,AM=AB,
∴AM=2EM,
∴∠BAM=30°,
在△ABM中,∠ABM=
(180°-∠BAM)=
(180°-30°)=75°,
∵矩形ABCD的∠ABC=90°,
∴∠CBM=90°-75°=15°,
∵N为CD的中点,
∴CN=
CD=
AB=BC,
∴△BCM是等腰直角三角形,
∴∠CBN=45°,
∴∠MBN=∠CBN-∠CBM=45°-15°=30°.
 解:如图,过点M作ME⊥AB于E,则EM=BC,
解:如图,过点M作ME⊥AB于E,则EM=BC,∵AB=2BC,AM=AB,
∴AM=2EM,
∴∠BAM=30°,
在△ABM中,∠ABM=
| 1 |
| 2 |
| 1 |
| 2 |
∵矩形ABCD的∠ABC=90°,
∴∠CBM=90°-75°=15°,
∵N为CD的中点,
∴CN=
| 1 |
| 2 |
| 1 |
| 2 |
∴△BCM是等腰直角三角形,
∴∠CBN=45°,
∴∠MBN=∠CBN-∠CBM=45°-15°=30°.
点评:本题考查了矩形的性质,等腰三角形的性质,直角三角形30°角所对的直角边等于斜边的一半以及等腰直角三角形的判定与性质,作出辅助线并求出∠BAM=30°是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,已知AC=2cm,△ABC的周长为8cm,K,F,N是△ABC与内切圆的切点,DE切⊙O于点M,且DE∥AC,求DE的长.
如图,在△ABC中,已知AC=2cm,△ABC的周长为8cm,K,F,N是△ABC与内切圆的切点,DE切⊙O于点M,且DE∥AC,求DE的长. 如图,一个有弹性的小球从点A下落到地面,弹起到点B后,再次落到地面又弹起到点C,已知弹起的高度是之前落下高度的80%.
如图,一个有弹性的小球从点A下落到地面,弹起到点B后,再次落到地面又弹起到点C,已知弹起的高度是之前落下高度的80%.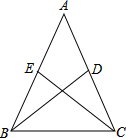 已知:如图,在△ABC中,AB=AC,BD,CE是△ABC的中线.
已知:如图,在△ABC中,AB=AC,BD,CE是△ABC的中线.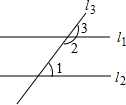 用反证法证明:两直线平行,同旁内角互补(填空).
用反证法证明:两直线平行,同旁内角互补(填空).