题目内容
 如图,在△ABC中,已知AC=2cm,△ABC的周长为8cm,K,F,N是△ABC与内切圆的切点,DE切⊙O于点M,且DE∥AC,求DE的长.
如图,在△ABC中,已知AC=2cm,△ABC的周长为8cm,K,F,N是△ABC与内切圆的切点,DE切⊙O于点M,且DE∥AC,求DE的长.考点:三角形的内切圆与内心
专题:
分析:因为AB,AC,BC,DM都是圆的切线,由得,DK=DM,EM=EN,AK=AF,CF=CN,EM=EN,此定理可以证明,以DK=DM为例,连接OD,因为角OKD=OMD=90,OD=OD,OM=OK,所以三角形OKD全等于OMD,所以DK=AD,再由已知条件即可求出DE的长.
解答:解:因为AB,AC,BC,DM都是圆的切线,
由得,DK=DM,EM=EN,AK=AF,CF=CN,EM=EN三角形ABC的周长=AB+BC+AC=BK+AK+AF+CF+CN+BN=8,
又因为,AC=AF+CF=AK+CN=2,代入上式,得BK+BN=4,
三角形BDE周长=BD+DE+BE=BD+DM+EM+BE,
又因为,DK=DM,EM=EN,所以,三角形BDE周长=BD+DK+BE+EN=BK+BN=4,
因为,DE‖AC,所以△BDE∽△BAC,
所以AC:DE=三角形ABC周长:三角形DBE周长=8:4=2,
所以DE=1.
由得,DK=DM,EM=EN,AK=AF,CF=CN,EM=EN三角形ABC的周长=AB+BC+AC=BK+AK+AF+CF+CN+BN=8,
又因为,AC=AF+CF=AK+CN=2,代入上式,得BK+BN=4,
三角形BDE周长=BD+DE+BE=BD+DM+EM+BE,
又因为,DK=DM,EM=EN,所以,三角形BDE周长=BD+DK+BE+EN=BK+BN=4,
因为,DE‖AC,所以△BDE∽△BAC,
所以AC:DE=三角形ABC周长:三角形DBE周长=8:4=2,
所以DE=1.
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,.三角形的内心就是三角形三个内角角平分线的交点.也考查了切线长定理.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
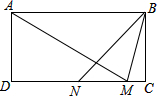 如图,在矩形ABCD中,AB=2BC,N为CD的中点,点M在CD上,且AM=AB,求∠MBN的度数.
如图,在矩形ABCD中,AB=2BC,N为CD的中点,点M在CD上,且AM=AB,求∠MBN的度数.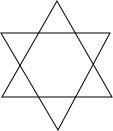 某村建造农民文化公园,将12个场馆排成6行,每行4个场馆.村委会将如图的设计方案公布后,引起一群初中生的好奇,他们纷纷设计出不少精美对称的图案,请你也试试把12个场馆设计成符合要求的轴对称图形.
某村建造农民文化公园,将12个场馆排成6行,每行4个场馆.村委会将如图的设计方案公布后,引起一群初中生的好奇,他们纷纷设计出不少精美对称的图案,请你也试试把12个场馆设计成符合要求的轴对称图形.