题目内容
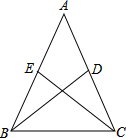 已知:如图,在△ABC中,AB=AC,BD,CE是△ABC的中线.
已知:如图,在△ABC中,AB=AC,BD,CE是△ABC的中线.(1)求证:BD=CE;
(2)改变题目中的一个条件,(1)的结论仍然成立吗?说明你的理由;
(3)请用文字叙述(2)的结论.
考点:全等三角形的判定与性质,等腰三角形的性质
专题:
分析:(1)根据条件可以得出AE=AD,证明△ADB≌△AEC就可以得出结论;
(2)若BD,CE是△ABC的高结论仍然成立;
(3)根据BD,CE是△ABC的高就可以得出∠ADB=∠AEC=90°,就可以AAS得出△ADB≌△AEC就可以得出结论.
(2)若BD,CE是△ABC的高结论仍然成立;
(3)根据BD,CE是△ABC的高就可以得出∠ADB=∠AEC=90°,就可以AAS得出△ADB≌△AEC就可以得出结论.
解答:证明:(1)∵BD,CE是△ABC的中线.
∴AD=
AC,AE=
AB.
∵AB=AC,
∴
AB=
AC,
∴AD=AE.
在△ADB和△AEC中,
,
∴△ADB≌△AEC(SAS),
∴BD=CE;
(2)若BD,CE是△ABC的高(1)的结论仍然成立.
理由:∵BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°.
在△ADB和△AEC中
,
∴△ADB≌△AEC(AAS),
∴BD=CE;
(3)已知:在△ABC中,AB=AC,BD,CE是△ABC的高,
结论:BD=CE.
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=AC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=AE.
在△ADB和△AEC中,
|
∴△ADB≌△AEC(SAS),
∴BD=CE;
(2)若BD,CE是△ABC的高(1)的结论仍然成立.
理由:∵BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°.
在△ADB和△AEC中
|
∴△ADB≌△AEC(AAS),
∴BD=CE;
(3)已知:在△ABC中,AB=AC,BD,CE是△ABC的高,
结论:BD=CE.
点评:本题考查了等腰三角形的性质的运用,全等三角形的判定及性质的运用,垂直的性质的运用,解答时运用等腰三角形的性质证明三角形全等是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
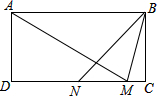 如图,在矩形ABCD中,AB=2BC,N为CD的中点,点M在CD上,且AM=AB,求∠MBN的度数.
如图,在矩形ABCD中,AB=2BC,N为CD的中点,点M在CD上,且AM=AB,求∠MBN的度数.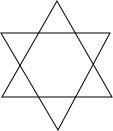 某村建造农民文化公园,将12个场馆排成6行,每行4个场馆.村委会将如图的设计方案公布后,引起一群初中生的好奇,他们纷纷设计出不少精美对称的图案,请你也试试把12个场馆设计成符合要求的轴对称图形.
某村建造农民文化公园,将12个场馆排成6行,每行4个场馆.村委会将如图的设计方案公布后,引起一群初中生的好奇,他们纷纷设计出不少精美对称的图案,请你也试试把12个场馆设计成符合要求的轴对称图形.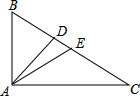 如图,在△ABC中,∠BAC=90°,AB=3cm,AC=4cm,AD是高线,AE是中线.
如图,在△ABC中,∠BAC=90°,AB=3cm,AC=4cm,AD是高线,AE是中线. 如图,在△ABC中,已知BC比AC长3cm,AB的垂直平分线交BC于点D,交AB于点E,△ACD的周长是15cm,求BC和AC的长.
如图,在△ABC中,已知BC比AC长3cm,AB的垂直平分线交BC于点D,交AB于点E,△ACD的周长是15cm,求BC和AC的长. 看图填空.
看图填空.