题目内容
4.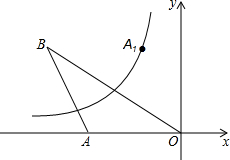 如图,在直角坐标系中,点A的坐标为(-10,0),点B在第二象限,AO=AB,OB=8$\sqrt{5}$,点A关于直线OB的对称点为A1,反比例函数y=$\frac{k}{x}$(k≠0,x<0)的图象经过点A1,则k=-48.
如图,在直角坐标系中,点A的坐标为(-10,0),点B在第二象限,AO=AB,OB=8$\sqrt{5}$,点A关于直线OB的对称点为A1,反比例函数y=$\frac{k}{x}$(k≠0,x<0)的图象经过点A1,则k=-48.
分析 连结AA1交OB于C点,连结OA1,如图,设B(x,y),利用两点间的距离公式得到(x+10)2+y2=102,x2+y2=(8$\sqrt{5}$)2,通过解方程组得到B点坐标为((-16,8),再证明AA1与OB互相垂直平分,根据线段的中点坐标公式得到C点坐标为(-8,4),再得到A1点的坐标为(-6,8),然后根据反比例函数图象上点的坐标特征求k的值.
解答 解:连结AA1交OB于C点,连结OA1,如图,
设B(x,y),
∵OA=AB=10,
∴(x+10)2+y2=102,
∵OB=8$\sqrt{5}$,
∴x2+y2=(8$\sqrt{5}$)2,
解方程组$\left\{\begin{array}{l}{(x+10)^{2}+{y}^{2}=1{0}^{2}}\\{{x}^{2}+{y}^{2}=(8\sqrt{5})^{2}}\end{array}\right.$得$\left\{\begin{array}{l}{x=-16}\\{y=8}\end{array}\right.$或$\left\{\begin{array}{l}{x=-16}\\{y=-8}\end{array}\right.$(舍去),
∴B点坐标为((-16,8),
∵AO=AB,
而点A关于直线OB的对称点为A1,
∴AA1与OB互相垂直平分,
∴C点坐标为(-8,4),
∴A1点的坐标为(-6,8),
把A1(-6,8)代入y=$\frac{k}{x}$得k=-6×8=-48.
故答案为-48.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了轴对称的性质和线段的中点坐标公式.

 如图,已知∠A=33°,∠B=75°,点C在直线AD上,则∠BCD为( )
如图,已知∠A=33°,∠B=75°,点C在直线AD上,则∠BCD为( )| A. | 147° | B. | 108° | C. | 105° | D. | 以上答案都不对 |

| A. | 51.5 | B. | 52 | C. | 52.5 | D. | 53 |
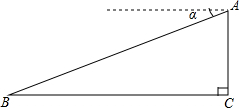 在寻找马航MH730航班的过程中,某搜寻飞机在空中A处发现海面上一块疑似漂浮目标B,从飞机上看目标B的俯角为α,此时飞机的飞行高度AC=1200米,tanα=$\frac{5}{12}$,则飞机距离疑似目标B的距离AB为( )
在寻找马航MH730航班的过程中,某搜寻飞机在空中A处发现海面上一块疑似漂浮目标B,从飞机上看目标B的俯角为α,此时飞机的飞行高度AC=1200米,tanα=$\frac{5}{12}$,则飞机距离疑似目标B的距离AB为( )| A. | 3120米 | B. | 2800$\sqrt{3}$米 | C. | 3260米 | D. | 3000$\sqrt{3}$米 |
| A. | x≥5 | B. | x≤5 | C. | x>5 | D. | x<5 |
| A. | 3.1415926 | B. | $\frac{22}{7}$ | C. | $\sqrt{2}$ | D. | (π-1)0 |
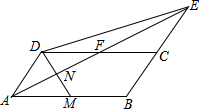 如图,在平行四边形ABCD中,AB=6,∠BAD的平分线与BC的延长线交于点E、与DC交于点F,且点F为边DC的中点,∠ADC的平分线交AB于点M,交AE于点N,连接DE
如图,在平行四边形ABCD中,AB=6,∠BAD的平分线与BC的延长线交于点E、与DC交于点F,且点F为边DC的中点,∠ADC的平分线交AB于点M,交AE于点N,连接DE