题目内容
5．
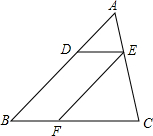如图，已知在△ABC中，点D、E、F分别是边AB、AC、BC上的点，DE∥BC，EF∥AB，且AD：DB=3：5，那么S△CEF：S四边形DBFE=5：6．
分析 先求出CF：BF，设△EFC的CF边上的高为h，利用面积公式计算即可．
解答 解：∵DE∥BF，EF∥BD，
∴四边形DBFE是平行四边形，
∴$\frac{AE}{EC}$=$\frac{AD}{DB}$=$\frac{3}{5}$，
∴$\frac{CF}{FB}$=$\frac{CE}{AE}$=$\frac{5}{3}$，
设△EFC的CF边上的高为h，
∴S△CEF：S四边形DBFE=$\frac{1}{2}$•CF•h：BF•h=$\frac{1}{2}$CF：BF=5：6，
故答案为5：6．
点评 本题考查相似三角形的判定和性质、三角形的面积．平行四边形的面积等知识，解题的关键是学会利用参数解决问题，属于中考常考题型．
练习册系列答案
相关题目
15．两个无理数的积一定是（ ）
| A． | 不是有理数 | B． | 不是无理数 | C． | 不是1 | D． | 不是0 |
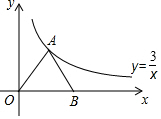已知反比例函数y=$\frac{3}{x}$在第一象限的图象如图所示，点A是在其图象上，点B为x轴正半轴上一点，连接AO、AB，且AO=AB，则S△AOB=3．
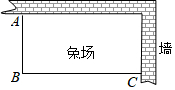某家庭农场要建一个长方形的养兔场，兔场的两边靠墙（两堵墙互相垂直，长度不限），另两边用木栏围成，木栏总长20米．
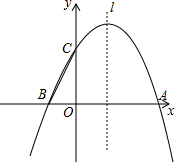如图，二次函数y=ax2-2ax+3的图象与x轴交于点A，B，与y轴交于点C，∠CBO的正切值是3．