题目内容
17.拓广探索:七年某班师生为了解决“22014个位上的数字是4.”这个问题,通过观察、分析、猜想、验证、归纳等活动,从而使问题得以解决,体现了从特殊到一般的数学思想方法.师生共同探索如下:(1)认真填空,仔细观察.
因为21=2,所以21个位上的数字是2;因为 22=4,所以22个位上的数字是4;因为 23=8,所以 23个位上的数字是8;因为 24=16,所以24个位上的数字是6;因为 25=32,所以 25个位上的数字是2;因为 26=64,所以26个位上的数字是4;
(2)小明是个爱动脑筋的学生,他利用上述方法继续探索,马上发现了规律,于是猜想:210个位上的数字是4,你认为对吗?
(3)利用上述得到的规律,可知:22013个位上的数字是2.
(4)利用上述研究数学问题的思想与方法,试求:32014个位上的数字是9.
分析 (1)根据指数运算法则直接求出各数即可;
(2)利用(1)中所求得出尾数每4个一循环分别为:2,4,8,6,进一步计算得出210个位上的数字是4;
(3)利用(2)中的规律得出答案;
(4)利用(2)中规律得出3的指数变化与尾数的关系.
解答 解:(1)因为21=2,所以21个位上的数字是2;
因为22=4,所以22个位上的数字是4;
因为23=8,所以23个位上的数字是8;
因为24=16,所以24个位上的数字是6;
因为25=32,所以25个位上的数字是2;
因为26=64,所以26个位上的数字是4;
(2)由(1)可得出:尾数每4个一循环分别为:2,4,8,6尾数每4个一循环,
10÷4=2…2,
则210个位上的数字与第2个数据相等是4;
(3)∵2013÷4=503…1,
∴22013个位上的数字与第1个尾数相等是2;
(4)因为31=3,所以31个位上的数字是3;
因为32=9,所以32个位上的数字是9;
因为33=27,所以33个位上的数字是7;
因为34=81,所以34个位上的数字是1;
因为35=243,所以35个位上的数字是3;
…
∴尾数每4个一循环,
∵2014÷4=503…2,
∴32014个位上的数字是9.
故答案为:4;16,6;32,2;64,4;2;9.
点评 此题主要考查了数字尾数特征,根据指数的变化得出位置的变化规律是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.小颖的妈妈在某玩具厂工作,厂里规定每个工人每周要生产某种玩具140个,平均每天生产20个,但由于种种原因,实际每天生产量与计划量相比有出入.下表是小颖妈妈某周的生产情况(超产记为正、减产记为负):
根据记录的数据求:
(1)小颖妈妈星期三生产玩具多少个?
(2)本周实际生产玩具多少个?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减产值 | +10 | -12 | -4 | +8 | -1 | +6 | 0 |
(1)小颖妈妈星期三生产玩具多少个?
(2)本周实际生产玩具多少个?
 [问题提出]
[问题提出]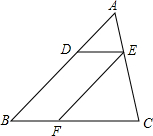 如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么S△CEF:S四边形DBFE=5:6.
如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么S△CEF:S四边形DBFE=5:6.