题目内容
11．
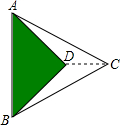如图，把一张等腰直角三角形纸片和一张等边三角形纸片叠在一起（等腰直角三角形的斜边等于等边三角形的边长），若AB=4$\sqrt{3}$，则CD=6-2$\sqrt{3}$．
分析 延长CD交AB于H，由AD=BD，AC=BC，于是得到CD垂直平分AB，根据线段垂直平分线的性质得到AH=BH=2$\sqrt{3}$，解直角三角形得到DH=$\frac{1}{2}$AB=2$\sqrt{3}$，根据勾股定理得到CH=$\sqrt{A{C}^{2}-A{H}^{2}}$=6，即可得到结论．
解答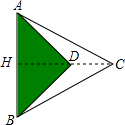 
解：延长CD交AB于H，
∵AD=BD，AC=BC，
∴CD垂直平分AB，
∴AH=BH=2$\sqrt{3}$，
∵∠ADB=90°，
∴DH=$\frac{1}{2}$AB=2$\sqrt{3}$，
∵AC=AB=4$\sqrt{3}$，
∴CH=$\sqrt{A{C}^{2}-A{H}^{2}}$=6，
∴CD=CH-DH=6-2$\sqrt{3}$，
故答案为：6-2$\sqrt{3}$．
点评 本题考查了等腰直角三角形的性质，等边三角形的性质，线段垂直平分线的判定，勾股定理，正确的作出辅助线是解题的关键．
练习册系列答案
相关题目
4．小敏到距家1500米的学校去上学，小敏出发10分钟后，小敏的爸爸立即去追小敏，且在距离学校60米的地方追上了她．已知爸爸比小敏的速度快100米/分，求小敏的速度．若设小敏的速度为x米/分，则根据题意所列方程正确的是（ ）
| A． | $\frac{1440}{x}=\frac{1440}{x+100}+10$ | B． | $\frac{1440}{x-100}-\frac{1440}{x}=10$ | ||
| C． | $\frac{1440}{x}=\frac{1440}{x-100}+10$ | D． | $\frac{1440}{x+100}-\frac{1440}{x}=10$ |
如图，△DEF是由等腰△ABC经过平移得到的，其中AB=AC，且A与D、B与E、C与F分别是对应点，若∠B=50°，则∠D=80°．
如图所示，P为⊙O外一点，PA、PB分别切⊙O于A、B，CD切⊙O于点E，分别交PA、PB于点C、D，若PA=15，则△PCD的周长为30．