题目内容
2.从-3,-2,-1,0,1,2,3这七个数中随机抽取一个数记为a,则a的值是不等式组$\left\{\begin{array}{l}3x+5>\frac{x}{2}\\ \frac{x}{3}<\frac{1}{2}+x\end{array}\right.$的解,但不是方程x2-3x+2=0的实数解的概率为$\frac{2}{7}$.分析 首先解不等式组,即可求得a的取值范围,解一元二次方程x2-3x+2=0,可求得a的值,然后直接利用概率公式求解即可求得答案.
解答 解:$\left\{\begin{array}{l}{3x+5>\frac{x}{2}①}\\{\frac{x}{3}<\frac{1}{2}+x②}\end{array}\right.$,
由①得:x>-2,
由②得:x>-$\frac{3}{4}$,
∵a的值是不等式组$\left\{\begin{array}{l}3x+5>\frac{x}{2}\\ \frac{x}{3}<\frac{1}{2}+x\end{array}\right.$的解,
∴a=0,1,2,3,
∵x2-3x+2=0,
∴(x-1)(x-2)=0,
解得:x1=1,x2=2,
∵a不是方程x2-3x+2=0的实数解,
∴a=0或3;
∴a的值是不等式组$\left\{\begin{array}{l}3x+5>\frac{x}{2}\\ \frac{x}{3}<\frac{1}{2}+x\end{array}\right.$的解,但不是方程x2-3x+2=0的实数解的概率为:$\frac{2}{7}$.
故答案为:$\frac{2}{7}$.
点评 此题考查了概率公式的应用、不等式组的解集以及一元二次方程的解法.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
15.一件商品a元,先涨价20%,然后再降价20%,此时这件商品的售价为( )
| A. | a元 | B. | 1.08a | C. | 0.96a | D. | 0.8a |
 苍溪嘉陵江三桥是连接苍溪老城与江南老区的一座下承式钢管混凝土柔性系杆拱桥,它的桥拱是抛物线形状,两桥墩的距离是240米,桥拱的拱高60米.
苍溪嘉陵江三桥是连接苍溪老城与江南老区的一座下承式钢管混凝土柔性系杆拱桥,它的桥拱是抛物线形状,两桥墩的距离是240米,桥拱的拱高60米.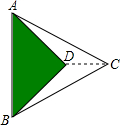 如图,把一张等腰直角三角形纸片和一张等边三角形纸片叠在一起(等腰直角三角形的斜边等于等边三角形的边长),若AB=4$\sqrt{3}$,则CD=6-2$\sqrt{3}$.
如图,把一张等腰直角三角形纸片和一张等边三角形纸片叠在一起(等腰直角三角形的斜边等于等边三角形的边长),若AB=4$\sqrt{3}$,则CD=6-2$\sqrt{3}$.