Question

【题目】在平面直角坐标系中，抛物线顶点为.

（1）点坐标为______（结果用表示）.

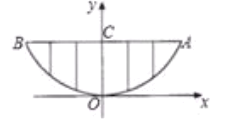
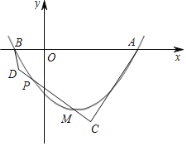
（2）当时，如图所示，该抛物线与轴交于，两点.为抛物线第二象限一点，过作的垂线，垂足为，为射线上一点，若，求；

（3），，若该抛物线与线段只有一个公共点，求的取值范围.

Answer 1

【答案】（1）；（2）；（3）.

【解析】

（1）化成顶点式即可求得；
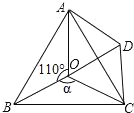
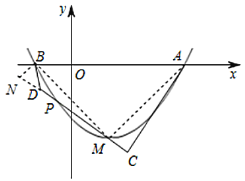
（2）过B点作BN⊥CD，交CD的延长线于N，连接BM、AM，求得点A，B，M的坐标，根据勾股定理的逆定理证得△ABM是等腰直角三角形，进而证得△AMC≌△MBN，即可证得BN=DN，得出△BDN是等腰直角三角形，根据三角形外角的性质即可求得∠BDM=135°；
（3）根据题意得到线段GH：,与联立得到令y′=,若抛物线y=与线段GH只有1个公共点，从而得到结论．

（1）∵抛物线，

∴顶点为为，故答案为；

（2）过点作，交的延长线于，连接、，

∵是抛物线的顶点，

∴，

当时，抛物线为，

令，则，解得，，

∴，，

∴，

∴，

∵，

∴，

∴，

∵，

∴是等腰直角三角形，

∴，

∴，

∵，

∴，

∴，

在和中

∴，

∴，，

∵，

∴，

∴，

∴，

∴是等腰直角三角形，

∴，

∴；

（3）∵，，

∴线段为，

与联立得：，

令，

若抛物线与线段只有1个公共点，

即函数在范围内只有一个零点，

当时，，

∵，∴此种情况不存在，

当时，，

解得.