Question

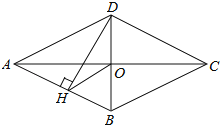
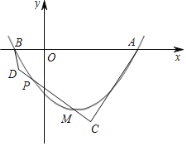
【题目】小南利用几何画板画图，探索结论，他先画∠MAN＝90°，在射线AM上取一点B，在射线AN上取一点C，连接BC，再作点A关于直线BC的对称点D，连接AD、BD，得到如图所示图形，移动点C，小南发现：当AD＝BC时，∠ABD＝90°；请你继续探索；当2AD＝BC时，∠ABD的度数是_____．

Answer 1

【答案】30°或150°

【解析】

分两种情况，取BC的中点E，连接AE，DE，依据直角三角形斜边上中线的性质，即可得到△ADE是等边三角形，进而依据轴对称的性质得出∠ABD的度数．

解：分两种情况：

如图，当AB＞AC时，取BC的中点E，连接AE，DE，

则AE＝DE＝BC，

即BC＝2AE＝2DE，

又∵BC＝2AD，

∴AD＝AE＝DE，

∴△ADE是等边三角形，

∴∠AED＝60°，

又∵BC垂直平分AD，

∴∠AEC＝30°，

又∵BE＝AE，

∴∠ABC＝∠AEC＝15°，

∴∠ABD＝2∠ABC＝30°；

如图，当AB＜AC时，同理可得∠ACD＝30°，

又∵∠BAC＝∠BDC＝90°，

∴∠ABD＝150°，

故答案为：30°或150°．