Question

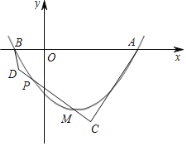
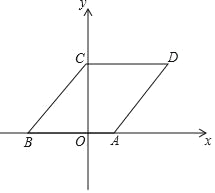
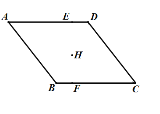
【题目】如图，菱形ABCD的边AD⊥EF，垂足为点E，点H是菱形ABCD的对称中心．若FC=，EF=DE，则菱形ABCD的边长为（　　）

A.B.3C.4D.5

Answer 1

【答案】A

【解析】

因为点H是菱形ABCD的对称中心，所以连接BD交EF于点H，故易证明△DEH≌△BFH，故可得DE＝BF，过D作DG⊥BC交BC于点G，可知四边形DEFG是长方形，设菱形ABCD的边长为x，在Rt△DGC中，用勾股定理列出关系x的方程，解出x的值，求出答案.

因为点H是菱形ABCD的对称中心，所以连接BD交EF于点H，∵，∴△DEH≌△BFH，故可得DE＝BF，过D作DG⊥BC交BC于点G，∴四边形DEFG是长方形，故DE＝FG，DG＝EF，设菱形ABCD的边长为x，故BF＝DE＝x－， DG＝EF＝（x－），CG＝BC－DE－BF＝x－2BF＝x－2（x－）＝－x，在Rt△DGC中，CG2＋DG2＝CD2，故（－x）2＋5（x－）2＝x2，解得：x1＝，x2＝（舍），故答案选A.