Question

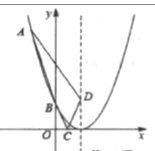
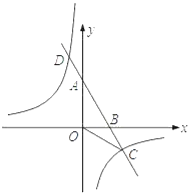
【题目】如图，已知A、B两点的坐标分别为A（0，2），B（2，0），直线AB与反比例函数y=的图象交于点C和点D（﹣1，a）．

（1）求直线AB和反比例函数的解析式；

（2）求∠ACO的度数．

Answer 1

【答案】（1）y＝－x＋2，y＝－；（2）30°

【解析】

试题（1）设直线AB的解析式为y=kx+b（k≠0），将A与B坐标代入求出k与b的值，确定出直线AB的解析式，将D坐标代入直线AB解析式中求出a的值，确定出D的坐标，将D坐标代入反比例解析式中求出m的值，即可确定出反比例解析式；（2）联立两函数解析式求出C坐标，过C作CH垂直于x轴，在直角三角形OCH中，由OH与HC的长求出tan∠COH的值，利用特殊角的三角函数值求出∠COH的度数，在三角形AOB中，由OA与OB的长求出tan∠ABO的值，进而求出∠ABO的度数，由∠ABO-∠COH即可求出∠ACO的度数．

试题解析：（1）设直线AB的解析式为y=kx+b（k≠0），

将A（0，2），B（2，0）代入得：，解得：.

∴直线AB解析式为.

将D（-1，a）代入直线AB解析式得：，则D（-1，）.

将D坐标代入中，得：m=.

∴反比例解析式为.

（2）联立两函数解析式得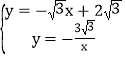：，解得：或.

∴C坐标为（3，）.

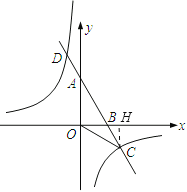
过点C作CH⊥x轴于点H，

在Rt△OHC中，CH=，OH=3，

∴.∴∠COH=30°.

在Rt△AOB中，，∴∠ABO=60°.

∴∠ACO=∠ABO-∠COH=30°．