题目内容
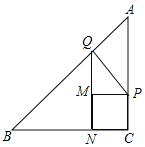
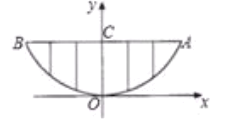
【题目】某校的围墙上端由- -段段相同的凹曲拱形栅栏组成，如图所示，栅栏的跨径
间，按相同的间距
米用
根立柱加固，拱高
为
米，以
为原点，所在的直线为
轴建立平面直角坐标系，根据以上的数据，则这段栅栏所需立柱的总长度（精确到
米）为（ ）
A. 
米B. 
米C. 
米D. 
米
【答案】C
【解析】
由题意可知，A点坐标为（0.6，0.6），代入y=ax2，可求出解析式．由于OC左右两边四根栅栏的底端横坐标已知，根据所求解析式，可计算出纵坐标，高度也就可以表示出来，计算即可．
解：抛物线顶点在原点，
设抛物线解析式为y=ax2，
把点A（0.6，0.6）代入解析式得a=
，
∴y=x2，
∴（0.2，
），（0.4，
）是该抛物线的两点，
∴这段栅栏所需立柱的总长度=（0.6-+0.6-）×2+0.6≈2.3（米）．
故选：C．
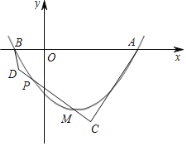
【题目】小明根据学习函数的经验，对函数y=x+
的图象与性质进行了探究．
下面是小明的探究过程，请补充完整：
（1）函数y=x+的自变量x的取值范围是_____．
（2）下表列出了y与x的几组对应值，请写出m，n的值：m=_____，n=_____；
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | 4 | … |
y | … | ﹣ | ﹣ | ﹣2 | ﹣ | ﹣ | m |
| 2 |
| n |
| … |
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
（4）结合函数的图象，请完成：
①当y=﹣
时，x=_____．
②写出该函数的一条性质_____．
③若方程x+=t有两个不相等的实数根，则t的取值范围是_____．
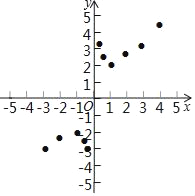
【题目】已知二次函数y=ax2+bx+c的y与x的部分对应值如表：则下列判断中正确的是（ ）
x | … | ﹣1 | 0 | 1 | 3 | … |
y | … | ﹣3 | 1 | 3 | 1 | … |
A. 抛物线开口向上B. 抛物线与y轴交于负半轴
C. 当x=4时，y＞0D. 方程ax2+bx+c=0的正根在3与4之间
