题目内容
13. 如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA的延长线上,∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为( )
如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA的延长线上,∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为( )| A. | 8 | B. | 16 | C. | 10 | D. | 20 |
分析 根据勾股定理先求出BC的长,再根据三角形中位线定理和直角三角形的性质求出DE和AE的长,进而由已知可判定四边形AEDF是平行四边形,从而不难求得其周长.
解答 解:在Rt△ABC中,
∵AC=6,AB=8,
∴BC=10,
∵E是BC的中点,
∴AE=BE=5,
∴∠BAE=∠B,
∵∠FDA=∠B,
∴∠FDA=∠BAE,
∴DF∥AE,
∵D、E分别是AB、BC的中点,
∴DE∥AC,DE=$\frac{1}{2}$AC=3,
∴四边形AEDF是平行四边形
∴四边形AEDF的周长=2×(3+5)=16.
故选:B.
点评 本题考查了三角形中位线定理的运用,熟悉直角三角形的性质、等腰三角形的判定以及平行四边形的判定.熟练运用三角形的中位线定理和直角三角形的勾股定理是解题的关键.

练习册系列答案
相关题目
1. 根据2011-2015年萧山区财政总收入(单位:亿元)统计图所提供的信息,下列判断正确的是( )
根据2011-2015年萧山区财政总收入(单位:亿元)统计图所提供的信息,下列判断正确的是( )
 根据2011-2015年萧山区财政总收入(单位:亿元)统计图所提供的信息,下列判断正确的是( )
根据2011-2015年萧山区财政总收入(单位:亿元)统计图所提供的信息,下列判断正确的是( )| A. | 2011-2015年财政总收入呈逐年增长 | |
| B. | 预计2016年的财政总收入约为253.43亿元 | |
| C. | 2012-2013年与2014-2015年的财政总收入下降率相同 | |
| D. | 2011-2012年的财政总收入增长率约为6.3% |
2.如果等边三角形的边长为8$\sqrt{2}$,那么等边三角形的中位线长为( )
| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
 如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=22,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=22,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒. 函数y=kx+b和函数y=ax+m的图象如图所示,求下列不等式(组)的解集
函数y=kx+b和函数y=ax+m的图象如图所示,求下列不等式(组)的解集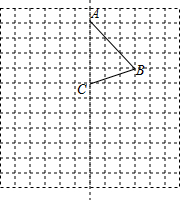 如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.
如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.