题目内容
8.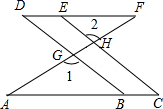 已知:如图,AC∥DF,直线AF分别与直线BD、CE相交于点G,H,∠1=∠2,求证:∠C=∠D.
已知:如图,AC∥DF,直线AF分别与直线BD、CE相交于点G,H,∠1=∠2,求证:∠C=∠D.解:∵∠1=∠2(已知)
∠1=∠DGH(对顶角相等 ),
∴∠2=∠DGH( 等量代换 )
∴DB∥EC(同位角相等,两直线平行)
∴∠C=∠DBA(两直线平行,同位角相等)
又∵AC∥DF(已知 )
∴∠D=∠ABG (两直线平行,内错角相等 )
∴∠C=∠D (等量代换 )
分析 求出∠2=∠DGH,根据平行线的判定得出DB∥EC,根据平行线的性质得出∠C=∠DBA,∠D=∠ABG,即可得出答案.
解答 解:∵∠1=∠2(已知)
∠1=∠DGH(对顶角相等)
∴∠2=∠DGH( 等量代换 )
∴DB∥EC(同位角相等,两直线平行)
∴∠C=∠DBA(两直线平行,同位角相等)
又∵AC∥DF(已知)
∴∠D=∠ABG (两直线平行,内错角相等)
∴∠C=∠D (等量代换),
故答案为:对顶角相等,∠DGH,DB,EC,∠DBA,已知,两直线平行,内错角相等,等量代换.
点评 本题考查了平行线的性质和判定的应用,能灵活运用定理进行推理是解此题的关键.

练习册系列答案
相关题目
19.下列计算中正确的是( )
| A. | x2•x4=x8 | B. | x3+x3=x6 | C. | (-m)2•(-m3)=-m5 | D. | (a3)3=a6 |
16.期末考试后,数学老师想制作一个统计图来了解一下本班数学考试各个分数段人数占班级总人数的百分比,最适合的统计图是( )
| A. | 条形统计图 | B. | 扇形统计图 | C. | 折线统计图 | D. | 以上都可以 |
13.一个数的算术平方根等于它本身,则这个数应是( )
| A. | 1 | B. | -1 | C. | 1或-1 | D. | 1或0 |
 如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=22,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=22,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.