题目内容
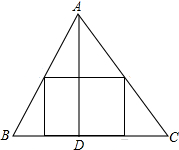如图，△ABC是一块铁皮，边BC=40cm，高AD=20cm，要用它才出一个矩形铁皮，能否使矩形的周长为48cm？若能，求出裁出矩形铁皮的长和宽；若不能，请说明理由．考点：相似三角形的应用,一元二次方程的应用
专题：
分析：利用相似三角形的判定与性质得出△AEF∽△ABC，进而求出即可．
解答：
解：设EF=MN=x，ME=FN=（24-x），
∵EF∥BC，
∴△AEF∽△ABC，
∴
=
，
∴
=
，
解得：x=8，
故24-x=16，
即矩形铁皮的长为16cm和宽为8cm．
解：设EF=MN=x，ME=FN=（24-x），∵EF∥BC，
∴△AEF∽△ABC，
∴
| AW |
| AD |
| EF |
| BC |
∴
| x |
| 40 |
| 20-(24-x) |
| 20 |
解得：x=8，
故24-x=16，
即矩形铁皮的长为16cm和宽为8cm．
点评：此题主要考查了相似三角形的判定与性质，得出△AEF∽△ABC是解题关键．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
如图，在四边形ABCD中，∠A+∠B=120°，AD=BC，以CD为边向外作等边△CDE，连接AE，BE．求证：△ABE为等边三角形．
如图，直线l1：y=