题目内容
如图,△ABC和△ADE都是以A为直角顶点的等腰直角三角形,点B、A、E在同一直线上.
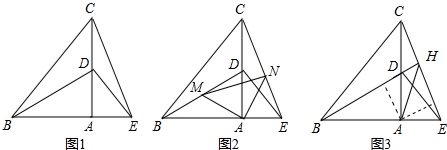
(1)求证:△ABD≌△ACE;
(2)如图2,设M,N分别是BD,CE的中点,求证:△AMN也是等腰直角三角形;
(3)如图3,延长BD交CE于H,求证:∠BHA=45°.

(1)求证:△ABD≌△ACE;
(2)如图2,设M,N分别是BD,CE的中点,求证:△AMN也是等腰直角三角形;
(3)如图3,延长BD交CE于H,求证:∠BHA=45°.
考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:(1)根据等腰直角三角形腰长相等和顶角为90°的性质即可证明△ABD≌△ACE;
(2)根据△ABD≌△ACE可得BD=CE,根据直角三角形中线性质可得AN=AM,再根据∠MBA=∠MAB即可求得∠MAN=90°,即可解题;
(3)作AM⊥BH,AN⊥CE,即可求得∠MAD=∠NAE,即可求证△AEN≌△ADM,即可解题.
(2)根据△ABD≌△ACE可得BD=CE,根据直角三角形中线性质可得AN=AM,再根据∠MBA=∠MAB即可求得∠MAN=90°,即可解题;
(3)作AM⊥BH,AN⊥CE,即可求得∠MAD=∠NAE,即可求证△AEN≌△ADM,即可解题.
解答:解:(1)在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)∵△ABD≌△ACE,
∴BD=CE,
∴∠ABD=∠ACE,
∵M,N分别是BD,CE的中点,BD,CE是RT△ABD和RT△ACE斜边中点,
∴AM=BM=MD,AN=CN=NE,
∴AM=AN,
∴∠ABM=∠BAM,∠ACN=∠CAN,
∴∠BAM=∠CAN,
∴∠MAN=90°,
∴△AMN为等腰直角三角形;
(3)作AM⊥BH,AN⊥CE,
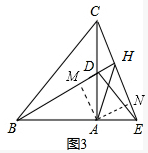
∵△ABD≌△ACE,
∴∠ADB=∠AEC,∠ABD=∠ACE,
∵∠ACE+∠AEC=90°,
∴∠ABD+∠AEC=90°,
∴∠BHE=90°,
∵∠AMH=∠ANH=90°,
∴∠MAN=90°,∵∠CAE=90°,
∴∠MAD=∠NAE,
在△AEN和△ADM中,
,
∴△AEN≌△ADM(ASA),
∴AM=AN,
∴矩形AMHN为正方形,
∴∠BHA=45°.
|
∴△ABD≌△ACE(SAS);
(2)∵△ABD≌△ACE,
∴BD=CE,
∴∠ABD=∠ACE,
∵M,N分别是BD,CE的中点,BD,CE是RT△ABD和RT△ACE斜边中点,
∴AM=BM=MD,AN=CN=NE,
∴AM=AN,
∴∠ABM=∠BAM,∠ACN=∠CAN,
∴∠BAM=∠CAN,
∴∠MAN=90°,
∴△AMN为等腰直角三角形;
(3)作AM⊥BH,AN⊥CE,

∵△ABD≌△ACE,
∴∠ADB=∠AEC,∠ABD=∠ACE,
∵∠ACE+∠AEC=90°,
∴∠ABD+∠AEC=90°,
∴∠BHE=90°,
∵∠AMH=∠ANH=90°,
∴∠MAN=90°,∵∠CAE=90°,
∴∠MAD=∠NAE,
在△AEN和△ADM中,
|
∴△AEN≌△ADM(ASA),
∴AM=AN,
∴矩形AMHN为正方形,
∴∠BHA=45°.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ABD≌△ACE是解题的关键.

练习册系列答案
相关题目
 如图,点A、B、C、D为⊙O上的点,∠ABC=90°,若AD=8,tan∠DBC=
如图,点A、B、C、D为⊙O上的点,∠ABC=90°,若AD=8,tan∠DBC=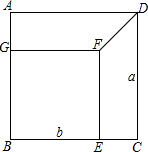 如图,将边长为a的正方形ABCD剪去一个边长为b的正方形BEFG,连接DF.根据四边形ABCD,BEFG,AGFD与ECDF的面积关系.你能推出一个什么样的结论?
如图,将边长为a的正方形ABCD剪去一个边长为b的正方形BEFG,连接DF.根据四边形ABCD,BEFG,AGFD与ECDF的面积关系.你能推出一个什么样的结论? a、b在数轴上对应的点如图所示:
a、b在数轴上对应的点如图所示: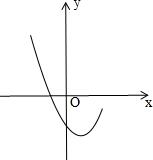 已知二次函数y=x2-2x+c的部分图象如图所示.
已知二次函数y=x2-2x+c的部分图象如图所示.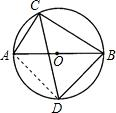 如图,AB是⊙O的直径,弦CD平分∠ACB,若AC+BC=6,则四边形ACBD的面积是
如图,AB是⊙O的直径,弦CD平分∠ACB,若AC+BC=6,则四边形ACBD的面积是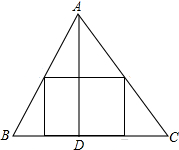 如图,△ABC是一块铁皮,边BC=40cm,高AD=20cm,要用它才出一个矩形铁皮,能否使矩形的周长为48cm?若能,求出裁出矩形铁皮的长和宽;若不能,请说明理由.
如图,△ABC是一块铁皮,边BC=40cm,高AD=20cm,要用它才出一个矩形铁皮,能否使矩形的周长为48cm?若能,求出裁出矩形铁皮的长和宽;若不能,请说明理由.