题目内容
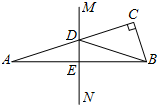如图，在△ABC中，∠C=90°，AB的垂直平分线MN分别交AC，AB于点D，E． 若∠CBD：∠DBA=3：1，则∠A=考点：线段垂直平分线的性质
专题：
分析：由线段垂直平分线的性质可知DB=DA，可得∠A=∠DBA，又由条件可知∠CBD=3∠A，则在Rt△ABC中可得∠A+∠A+3∠A=90°，可求得∠A．
解答：解：
∵MN为AB垂直平分线，且D在MN上，
∴DA=DB，
∴∠A=∠DBA，
∵∠CBD：∠DBA=3：1，
∴∠CBD=3∠DBA=3∠A，
∵∠C=90°，
∴∠A+∠ABC=90°，
即∠A+∠A+3∠A=90°，
解得∠A=18°，
故答案为：18°．
∵MN为AB垂直平分线，且D在MN上，
∴DA=DB，
∴∠A=∠DBA，
∵∠CBD：∠DBA=3：1，
∴∠CBD=3∠DBA=3∠A，
∵∠C=90°，
∴∠A+∠ABC=90°，
即∠A+∠A+3∠A=90°，
解得∠A=18°，
故答案为：18°．
点评：本题主要考查线段垂直平分线的性质，掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键，注意三角形内角和定理及方程思想的应用．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
一辆旅游车从大理返回昆明，旅游车距昆明的路程y（千米）与行驶时间x（小时）的函数关系如图所示：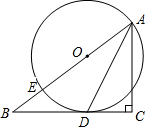
已知：如图，在Rt△ABC中，∠C=90°，点E在斜边AB上，以AE为直径的⊙O与BC边相切于点D，联结AD．
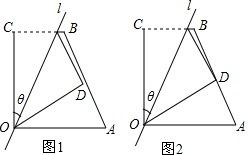如图1，四边形OABC中，OA=a，OC=5，BC=3，∠AOC=∠BCO=90°，经过点O的直线l将四边形分成两部分，直线l与OC所成的角设为θ，将四边形OABC的直角∠OCB沿直线l折叠，点C落在点D处（如图1）．