题目内容
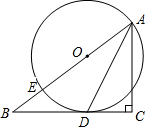 已知:如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC边相切于点D,联结AD.
已知:如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC边相切于点D,联结AD.(1)求证:AD是∠BAC的平分线;
(2)若AC=3,BC=4,求⊙O的半径.
考点:切线的性质,相似三角形的判定与性质
专题:
分析:(1)连接OD.根据圆的半径都相等的性质及等边对等角的性质知:∠1=∠2;再由切线的性质及平行线的判定与性质证明∠1=∠3;最后由角平分线的性质证明结论;
(2)在Rt△ABC中,由“AC=3,BC=4”求得AB=5;然后在Rt△ODB中,利用∠B的正切值求得
;设一份为x,则OD=OA=3x,则BD=4x,OB=5x.列出关于x的方程,解方程即可.
(2)在Rt△ABC中,由“AC=3,BC=4”求得AB=5;然后在Rt△ODB中,利用∠B的正切值求得
| OD |
| BD |
解答:(1)证明:连接OD,
∴OD=OA,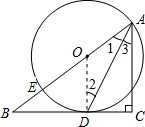
∴∠1=∠2,
∵BC为⊙O的切线,
∴∠ODB=90°,
∵∠C=90°,
∴∠ODB=∠C,
∴OD∥AC,
∴∠3=∠2,
∴∠1=∠3,
∴AD是∠BAC的平分线.
(2)解:在Rt△ABC中,∠C=90°,AC=3,BC=4,
∴由勾股定理得 AB=5.
在Rt△ODB中,tanB=
,
设一份为x,则OD=OA=3x,则BD=4x,OB=5x,
∴AB=8x,
∴8x=5,
解得x=
,
∴半径OA=
.
∴OD=OA,

∴∠1=∠2,
∵BC为⊙O的切线,
∴∠ODB=90°,
∵∠C=90°,
∴∠ODB=∠C,
∴OD∥AC,
∴∠3=∠2,
∴∠1=∠3,
∴AD是∠BAC的平分线.
(2)解:在Rt△ABC中,∠C=90°,AC=3,BC=4,
∴由勾股定理得 AB=5.
在Rt△ODB中,tanB=
| OD |
| BD |
设一份为x,则OD=OA=3x,则BD=4x,OB=5x,
∴AB=8x,
∴8x=5,
解得x=
| 5 |
| 8 |
∴半径OA=
| 15 |
| 8 |
点评:本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
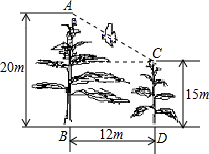 如图,美丽的校园里有两棵树,小鸟从C处飞到A处,小鸟至少飞行
如图,美丽的校园里有两棵树,小鸟从C处飞到A处,小鸟至少飞行 如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=a,ON、CD分别为两圆的半径,则阴影部分的面积为
如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=a,ON、CD分别为两圆的半径,则阴影部分的面积为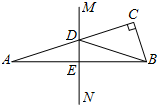 如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E. 若∠CBD:∠DBA=3:1,则∠A=
如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E. 若∠CBD:∠DBA=3:1,则∠A=