题目内容
某种药品的价格经过两次连续降价后,由每盒100元下调至64元.假设每次降价的百分率是x,列出方程 .
考点:由实际问题抽象出一元二次方程
专题:增长率问题
分析:关系式为:药品原价×(1-降低的百分比)2=下调后的价格,即可得出答案.
解答:解:设该药品平均每次降价的百分率是x,根据题意得出:
100(1-x)2=64.
故答案为:100(1-x)2=64.
100(1-x)2=64.
故答案为:100(1-x)2=64.
点评:此题主要考查了由实际问题抽象出一元二次方程,得到下调后价格的关系式是解决本题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
设a、b是任意两个实数,且a<b.我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当a≤x≤b时,有a≤y≤b,我们就称此函数是闭区间[a,b]上的“闭函数”.若二次函数y=
x2-2x是区间[m,n]上的“闭函数”,则实数m、n值分别为( )
| 1 |
| 2 |
A、m=1-
| ||||
B、m=-1,n=2或m=1-
| ||||
| C、m=-2,n=6 | ||||
D、m=-2,n=6或m=1-
|
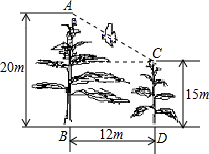 如图,美丽的校园里有两棵树,小鸟从C处飞到A处,小鸟至少飞行
如图,美丽的校园里有两棵树,小鸟从C处飞到A处,小鸟至少飞行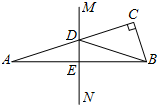 如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E. 若∠CBD:∠DBA=3:1,则∠A=
如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E. 若∠CBD:∠DBA=3:1,则∠A=