题目内容
已知3x2+2y2=6x,x,y是实数,求x2+y2的最大值和最小值.
考点:二次函数的最值
专题:
分析:整理得到x2+y2的表达式,再根据二次函数的最值问题和平方数非负数的性质解答.
解答:解:∵3x2+2y2=6x,
∴x2+y2=
(-x2+6x)=-
(x-3)2+
,
∵-
<0,
∴当x=3时,x2+y2有最大值
,
∵x2+y2≥0,
∴当x=y=0时,x2+y2有最小值0.
∴x2+y2=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
∵-
| 1 |
| 2 |
∴当x=3时,x2+y2有最大值
| 9 |
| 2 |
∵x2+y2≥0,
∴当x=y=0时,x2+y2有最小值0.
点评:本题考查了二次函数的最值问题,整理出x2+y2的表达式,考虑利用二次函数求解是解题的关键.

练习册系列答案
相关题目
 如图,△ABC中,AB=AC,AD平分∠BAC,则下列结论不一定正确的是( )
如图,△ABC中,AB=AC,AD平分∠BAC,则下列结论不一定正确的是( )| A、∠B=∠C |
| B、AB=2BD |
| C、AD⊥BC |
| D、BD=CD |
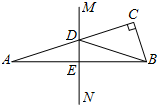 如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E. 若∠CBD:∠DBA=3:1,则∠A=
如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E. 若∠CBD:∠DBA=3:1,则∠A=