题目内容
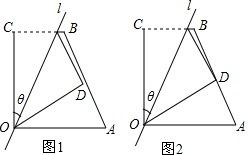 如图1,四边形OABC中,OA=a,OC=5,BC=3,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处(如图1).
如图1,四边形OABC中,OA=a,OC=5,BC=3,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处(如图1).(1)若折叠后点D恰为AB的中点(如图2),求θ的值;
(2)若θ=45°,四边形OABC的直角∠OCB沿直线l折叠后,点C落在四边形OABC的边AB上,求a的值.
考点:翻折变换(折叠问题)
专题:
分析:(1)如图2,作辅助线,首先证明DM=DN,进而证明∠AOD=∠DOM=∠MOC=θ,问题即可解决.
(2)如图3,运用翻折变换的性质得到OE=OC=5,DE=BC=3;证明AE=DE,问题即可解决.
(2)如图3,运用翻折变换的性质得到OE=OC=5,DE=BC=3;证明AE=DE,问题即可解决.
解答:解:(1)如图1,连接MD并延长,交OA的延长线于点N;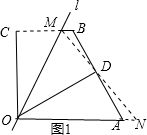
∵BM∥AN,
∴△BMD∽△AND,
∴
=
,而BD=AD,
∴MD=ND;
由题意得:∠ODM=∠C=90°,∠MOD=∠MOC=θ;
∴OD是线段MN的垂直平分线,
∴OM=ON,
∴OD平分∠MON,
∴∠AOD=∠DOM=∠MOC=θ,
∵∠AOC=90°,
∴θ=30°.
(2)如图2,由题意得: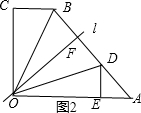
l⊥AB,OE=OC=5,DE=BC=3;
∠OED=∠C=90°;
∵∠AOF=45°,l⊥AB,
∴∠A=45°,∠ADE=90°-45°=45°,
∴∠A=∠ADE,
∴AE=DE=3,
∴OA=5+3=8,
即a的值为8.

∵BM∥AN,
∴△BMD∽△AND,
∴
| MD |
| ND |
| BD |
| AD |
∴MD=ND;
由题意得:∠ODM=∠C=90°,∠MOD=∠MOC=θ;
∴OD是线段MN的垂直平分线,
∴OM=ON,
∴OD平分∠MON,
∴∠AOD=∠DOM=∠MOC=θ,
∵∠AOC=90°,
∴θ=30°.
(2)如图2,由题意得:

l⊥AB,OE=OC=5,DE=BC=3;
∠OED=∠C=90°;
∵∠AOF=45°,l⊥AB,
∴∠A=45°,∠ADE=90°-45°=45°,
∴∠A=∠ADE,
∴AE=DE=3,
∴OA=5+3=8,
即a的值为8.
点评:该题以梯形为载体,以翻折变换为方法,以梯形的性质、相似三角形的判定及其性质、线段垂直平分线的性质等几何知识点的考查为核心构造而成;对对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设a、b是任意两个实数,且a<b.我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当a≤x≤b时,有a≤y≤b,我们就称此函数是闭区间[a,b]上的“闭函数”.若二次函数y=
x2-2x是区间[m,n]上的“闭函数”,则实数m、n值分别为( )
| 1 |
| 2 |
A、m=1-
| ||||
B、m=-1,n=2或m=1-
| ||||
| C、m=-2,n=6 | ||||
D、m=-2,n=6或m=1-
|
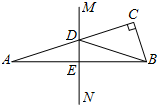 如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E. 若∠CBD:∠DBA=3:1,则∠A=
如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E. 若∠CBD:∠DBA=3:1,则∠A= 如图,在Rt△ABC中,∠C=90°,BC=5,若以点C为圆心,CB长为半径的圆恰好经过AB的中点D,则AB的长等于
如图,在Rt△ABC中,∠C=90°,BC=5,若以点C为圆心,CB长为半径的圆恰好经过AB的中点D,则AB的长等于