题目内容

9．已知关于x 的一元二次方程x2-m=2x有两个不相等的实数根，则（　　）
A．m＜-1B．m＜-2C．m＞-1D．m＞1

分析 先把方程化为一般式，再根据判别式的意义得到（-2）2-4（-m）＞0，然后解不等式即可．

解答 解：方程化为程x2-2x-m=0，
根据题意得△=（-2）2-4（-m）＞0，
解得m＞-1．
故选C．

点评 本题考查了根的判别式：一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：当△＞0时，方程有两个不相等的两个实数根；当△=0时，方程有两个相等的两个实数根；当△＜0时，方程无实数根．

练习册系列答案
相关题目
2．计算：1+（-2）+3+（-4）+…+2011+（-2012）．
20．直角三角形的两条边长分别为$\sqrt{15}$和$\sqrt{10}$，则第三边的长为5或$\sqrt{5}$．
17．竖直上抛物体的高度h和时间t的关系式为：h=20t-5t2，请回答：
（1）经过2秒后，该物体离地20米； 
（2）经过4秒后，该物体落回地面．
4．某商场销售一批衬衫，预期每件赢利40元．，为了扩大销量，尽快减少库存，商场决定采取适当的降价措施．经过市场调查发现，如果每件衬衫降价x元，每天的销售量y（件）与降价x（元）之间的关系是y=20+2x．利润为Q元．
（1）当每件降价5元时，每天的销量及销售利润分别是多少？
（2）若商场平均每天赢利1200元，每件衬衫应降价多少元？
14．方程x2=k有两个不相等的实数根，则k的取值范围是k＞0．
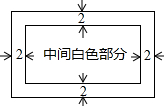1．如图，小红用一张周长为88cm的长方形白纸做一张贺卡，长方形白纸内部的四周涂上宽为2cm的彩色花边．
（1）求彩色花边的面积；
（2）若中间白色部分的面积是长方形白纸面积的$\frac{2}{3}$，求长方形白纸的边长．
18．解方程组
①$\left\{\begin{array}{l}{2x-3y=1}\\{x+2y=4}\end{array}\right.$     
②$\left\{\begin{array}{l}{\frac{x}{2}+\frac{y}{3}=16}\\{\frac{x}{3}-\frac{y}{4}=5}\end{array}\right.$．
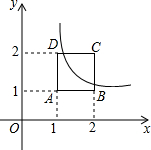17．如图，反比例函数y=$\frac{k}{x}$的图象与正方形ABCD在BC和CD边上相交．已知A（1，1），C（2，2），则k的值可能是（　　）
A．1B．2C．3D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网