题目内容
18.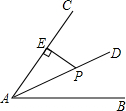 如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E,且PE=3,AE=5.有一点F在边AB上运动,当运动到某一位置时△FAP面积恰好是△EAP面积的2倍,则此时AF的长是( )
如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E,且PE=3,AE=5.有一点F在边AB上运动,当运动到某一位置时△FAP面积恰好是△EAP面积的2倍,则此时AF的长是( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
分析 过P作PM⊥AB于M,根据角平分线性质求出PM=3,根据已知得出关于AF的方程,求出方程的解即可.
解答 解:
过P作PM⊥AB于M,
∵点P是∠BAC的平分线AD上一点,PE⊥AC于点E,且PE=3,
∴PM=PE=3,
∵AE=5,△FAP面积恰好是△EAP面积的2倍,
∴$\frac{1}{2}$×AF×3=2×$\frac{1}{2}$×5×3,
∴AF=10,
故选A.
点评 本题考查了角的平分线性质,三角形面积公式的应用,能正确作出辅助线后得出关于AF的方程是解此题的关键,注意:角平分线上的点到角两边的距离相等.

练习册系列答案
相关题目
7.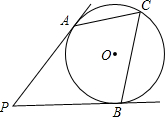 如图所示,PA,PB切⊙O于点A,B,C是$\widehat{ACB}$上的点,∠C=64°,则∠P的度数为.
如图所示,PA,PB切⊙O于点A,B,C是$\widehat{ACB}$上的点,∠C=64°,则∠P的度数为.
 如图所示,PA,PB切⊙O于点A,B,C是$\widehat{ACB}$上的点,∠C=64°,则∠P的度数为.
如图所示,PA,PB切⊙O于点A,B,C是$\widehat{ACB}$上的点,∠C=64°,则∠P的度数为.| A. | 26° | B. | 62° | C. | 65° | D. | 52° |
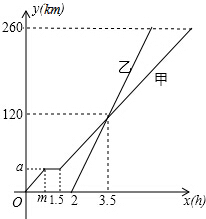 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(休息前后的速度一致),如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象.请根据图象提供的信息解答下列各题:
甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(休息前后的速度一致),如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象.请根据图象提供的信息解答下列各题: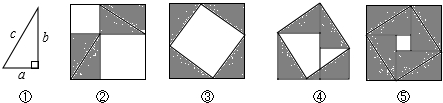
 如图,按此规律,第673行最后一个数是2017.
如图,按此规律,第673行最后一个数是2017.