题目内容
7.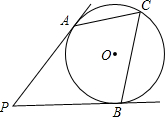 如图所示,PA,PB切⊙O于点A,B,C是$\widehat{ACB}$上的点,∠C=64°,则∠P的度数为.
如图所示,PA,PB切⊙O于点A,B,C是$\widehat{ACB}$上的点,∠C=64°,则∠P的度数为.| A. | 26° | B. | 62° | C. | 65° | D. | 52° |
分析 连接OA和OB,根据切线的性质可得∠PAO=∠PBO=90°,又根据同弧所对的圆心角等于它所对圆周角的2倍,由∠ACB的度数求出∠AOB的度数,在四边形APBO中,根据四边形的内角和为360°,即可求出所求角的度数.
解答 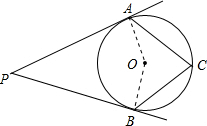 解:连接OA与OB,
解:连接OA与OB,
∵PA与PB为圆O的切线,
∴∠PAO=∠PBO=90°,
又$\widehat{AB}=\widehat{AB}$,∴∠AOB=2∠ACB=128°,
在四边形APBO中,∠APB=360°-90°-90°-128°=52°.
故选D.
点评 此题考查了切线的性质,圆周角定理及四边形的内角和.见了有切线,圆心切点连是此类题解答中运用较突出的一种技巧.本题的解题方法称为“构图建模计算法”,即构造四边形,借助四边形的内角和解决问题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
18.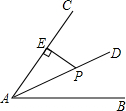 如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E,且PE=3,AE=5.有一点F在边AB上运动,当运动到某一位置时△FAP面积恰好是△EAP面积的2倍,则此时AF的长是( )
如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E,且PE=3,AE=5.有一点F在边AB上运动,当运动到某一位置时△FAP面积恰好是△EAP面积的2倍,则此时AF的长是( )
 如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E,且PE=3,AE=5.有一点F在边AB上运动,当运动到某一位置时△FAP面积恰好是△EAP面积的2倍,则此时AF的长是( )
如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E,且PE=3,AE=5.有一点F在边AB上运动,当运动到某一位置时△FAP面积恰好是△EAP面积的2倍,则此时AF的长是( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
15. 如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=20°,则∠CDE=( )
如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=20°,则∠CDE=( )
 如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=20°,则∠CDE=( )
如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=20°,则∠CDE=( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
2.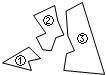 某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么可行的办法是( )
某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么可行的办法是( )
 某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么可行的办法是( )
某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么可行的办法是( )| A. | 带①③去 | B. | 带①去 | C. | 带②去 | D. | 带③去 |
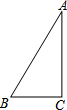 如图,已知Rt△ABC中,∠C=90°,∠A=30°,在直线BC或AC上取一点P,使得△PAB是等腰三角形,则符合条件的P点有( )
如图,已知Rt△ABC中,∠C=90°,∠A=30°,在直线BC或AC上取一点P,使得△PAB是等腰三角形,则符合条件的P点有( )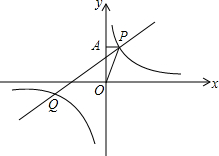 如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+4的图象交于P,Q两点,并且P点的纵坐标为6,直线y=ax+4交y轴于点A,且S△POA=4.
如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+4的图象交于P,Q两点,并且P点的纵坐标为6,直线y=ax+4交y轴于点A,且S△POA=4.