题目内容
8．已知⊙O的半径为5，点A是直线CD上一点，且OA=5，试问直线CD与⊙O是什么位置关系？分析 分为OA⊥CD和OA不垂直于CD两种情况，然后依据d和r的关系进行判断即可．
解答 解：当OA⊥CD时，d=r=5，直线CD与⊙O相切；
当OA不垂直于CD时，由垂线段最短可知d＜OA，
∴d＜r．
∴CD与⊙O相交．
综上所述，当OA⊥CD时，直线CD与⊙O相切；当OA不垂直于CD时，CD与⊙O相交．
点评 本题主要考查的是直线和圆的位置关系，分类讨论是解题的关键．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
18．
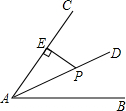如图，点P是∠BAC的平分线AD上一点，PE⊥AC于点E，且PE=3，AE=5．有一点F在边AB上运动，当运动到某一位置时△FAP面积恰好是△EAP面积的2倍，则此时AF的长是（ ）
如图，点P是∠BAC的平分线AD上一点，PE⊥AC于点E，且PE=3，AE=5．有一点F在边AB上运动，当运动到某一位置时△FAP面积恰好是△EAP面积的2倍，则此时AF的长是（ ）| A． | 10 | B． | 8 | C． | 6 | D． | 4 |
13．已知3y-2x=0，则（x+y）：（x-y）的值等于（ ）
| A． | $\frac{1}{5}$ | B． | 5 | C． | -5 | D． | -$\frac{1}{5}$ |